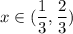1)6cosx+5sinx^2-6=0
2) 2log1/9 2-3x/x> -1
Другие вопросы по теме Алгебра
Популярные вопросы
- 4. ( 0, ) Обчислити площу прямокутника зі сторонами 4,5см і 6см. а) 27см2;...
1 - Дайте розгорнуту відповідь на одне із запропонованих запитань...
3 - Составьте любую задачу на тему давление с с решением и с условием...
1 - 10. Внук Амира Темура Мирзо Улугбек, «царственныйзвездочет», один из величайших...
2 - 1. Укажите неверные утверждения. А) Определение не обособляется, если...
3 - а то чет сложно да и я не много туповат...
1 - Задание 3. Переведите на английский, употребляя PresentPerfect. 1. Он...
2 - ть з завданням Перепишіть речення, підкресліть усі члени, зробіть синтаксичний...
1 - В каких предложениях выделенные слова являются определениями? 1.Время...
3 - В чём суть теории Джона Кейнса: правительства всех стран должны бороться...
1
с учётом D(f):