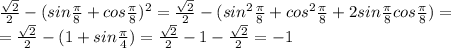1) 2sinп/8*cosп/8 2)sinп/8*cosп/8+1/4 3)cos^2*п/8-sin^2*п/8 4)корень из 2/2-(cosп/8+sinп/8)^2
Другие вопросы по теме Алгебра
Популярные вопросы
- Мозг человека гибок, но компьютеры быстрее выполняют различные вычеслительные...
1 - Перевидите текст на . geil cool! ich alleine im urlaub. ohne eltern, die...
2 - Как вы пониманиете слова найти себя в жизни...
3 - (x-2)² - 2*(x+1)²=(3-x)(3+x) решите у меня не получается 14 б...
2 - №1 какую из следующих дробей нельзя к знаменателю 100? 1)9/25 2)14/15...
1 - Масса пустого портфеля в 14,5 раза меньше массы книг. портфель вместе...
2 - Стрелки ирис белки село пропасть слова сочитание...
3 - Перевидите на 1 мне так же как и тебе 11 лет . 2 нет ,у меня нет животных...
3 - Придумайте к 5 формулам сокращённого умножения 35 примеров. к каждой формуле...
1 - 1)какую роль играет в вашей жизни книга? 2)зачем писатели обращались к...
2
1) 2sinП/8*cosП/8 - это формула двойного угла
2)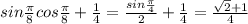
3) cos^2*П/8-sin^2*П/8 - это формула двойного угла
4)