1. Математика
  2. Задание из ЕГЭ Найдете все

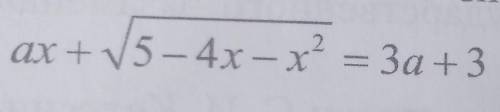
Задание из ЕГЭ
Найдете все значения а, при каждом из которых уравнение имеет один корень


Задание из ЕГЭ Найдете все значения а, при каждом из которых уравнение имеет один корень

nurgi12345 nurgi12345    1   14.07.2021 12:26    1

Ответы
MrLukz228 MrLukz228  13.08.2021 13:44

(см. объяснение)

Пошаговое объяснение:

ax+\sqrt{5-4x-x^2}=3a+3\\\sqrt{5-4x-x^2}=a(3-x)+3

Слева видим функцию без параметра, а справа параметрическая прямая, вращающаяся вокруг точки (3;\; 3). В таких случаях удобно строить отдельно левую (фиксированную) часть уравнения и правую (параметрическую) в координатах (x;\;y).

Для наглядности можно записать так:

\left\{\begin{array}{c}y=\sqrt{5-4x-x^2}\\y=a(3-x)+3\end{array}\right;

Понятно, что в первой строке системы у нас график полуокружности, достигающий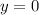 y=0 при x=-5 или x=1.

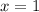После его построения будем вращать прямую вокруг точки (3;\; 3) и искать удовлетворяющие условию расположения.

(см. прикрепленный файл)

В первом случае прямая касается полуокружности в ее верхней точке, так как наибольшее значение будет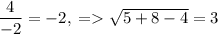  \dfrac{4}{-2}=-2,\;=\sqrt{5+8-4}=3. В этом случае a=0.

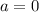Во втором случае прямая проходит через точки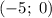 (-5;\;0) и (1;\;0).

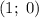Найдем соответствующие значения параметра:

0=a(3+5)+3,\;=\;a=-\dfrac{3}{8}\\\\0=a(3-1)+3,\;=\;a=-\dfrac{3}{2}

Теперь осталось только сформировать ответ:

При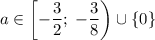 a\in\left[-\dfrac{3}{2};\;-\dfrac{3}{8}\right)\cup\left\{0\right\} исходное уравнение имеет ровно один корень.

Задание выполнено!


Задание из ЕГЭ Найдете все значения а, при каждом из которых уравнение имеет один корень
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
11nastyaaaaa11 11nastyaaaaa11  15.04.2020 10:52
. Автобус преодолел за первый час 40% пути, осталось еще90 км. Какова длина всего намеченного пути?​...
Прлплмопо Прлплмопо  15.04.2020 10:52
Решите пример с решением. (0,7:0,35)²-3,2·0,4+1,28=...
16912 16912  15.04.2020 10:52
Б) Витя пробежал х м со скоростью у м/мин. За какое времяон пробежал это расстояние...
aleksandrbersh0 aleksandrbersh0  15.04.2020 10:52
Пиктограммы задачи банан 6,яблок 6, апельсин 3,груши...
dndzanton dndzanton  15.04.2020 10:54
В координатной системе дана точка А(11;4;4). Определи координаты точек, в которые переходит точка А в зеркальной симметрии​...
arsjaja arsjaja  15.04.2020 10:54
Квадрокоптер b км сағ жылдамдықпен aсағ ұшты.Осы уақыт ішінде ол қандай қашықтықты ұшып өтті?​...
SonyaCooling SonyaCooling  15.04.2020 10:54
Высота прямоугольного параллелепипеда равна 6 см. Ширина этого параллелепипеда на 3,5 см меньше высоты и на 1,3 см меньше его длины. Найдите объем параллелепипеда....
брагим брагим  15.04.2020 10:54
Разность смежных сторон параллелограмма 11 см, периметр 58 см. Найдите его меньшую сторону....
temachbatman temachbatman  15.04.2020 10:54
Известно, что из точек А(0; 3), В(-2; -5), С(1; 7), К(3; -2) три принадлежат графику одной и той же линейной функции у=kx+b. Найдите k....
Fura44 Fura44  15.04.2020 10:54
Задание 1168 (составить чертеж)...

Популярные вопросы