Вычислите площадь фигуры, ограниченной линиями: y=4x-5 y=0 x=-3 x=-2
Другие вопросы по теме Математика
Популярные вопросы
- 9. а ) Бархан құмнан қашып , көшіп кеткісі келеді ; ә ) Бархан құмның аянышты халін...
1 - на первой картинке как надо делать на второй задание дальше всё для тех кто не увидел...
3 - Помгите Какое событие в истории россии 1920-1930 гг вы считаете значимым в чем значение...
2 - Выполни задания начерти числовай луч отметь на нем дроби...
2 - Задание 4. На контурной карте отметьте Скандина- вию, остров Рюген, Ладогу, Новгород....
1 - 1. Посадить одного из учеников на стул. Предложить ему поло- ожить ногу на ногу.2....
1 - написать рецепт блюда из 10 предложений на Русском блюдо любое...
3 - (Third conditional) If he (tell) me the truth I (forgive) him....
2 - Есе за темою: Які людські якості більше потрібні сучасній молоді? З прикладами ...
2 - 5. Падеж имен прилагательных во множественном чис. А) падежамВ) окончанию прилагательныхС)...
3
Для решения подобных задач часто используют формулу Ньютона-Лейбница:
Да, мы здесь считаем интеграл для функции (как результат приравнивания
(как результат приравнивания 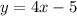 и
и 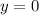 ). При этом,
). При этом,  и
и 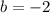 .
.
Таким образом, искомая площадь равна (ед²).
(ед²).
Но можно было и заметить (смотрите рисунок ниже), что у нас получилась трапеция ("обычная", не "криволинейная"), площадь которой равна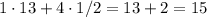 ( {площадь четырехугольника} + {площадь треугольника} ).
( {площадь четырехугольника} + {площадь треугольника} ).
ответ : 15 .