Вычислить производную функции.
Другие вопросы по теме Математика
Популярные вопросы
- Сума двох чисел дорівнює 246, а різниця — 32. Знайдіть ці числа...
3 - Довжина садової ділянки прямокутної форми дорівнює 75 м, а ширина — на 5...
1 - Сума двох чисел дорівнює 450, а їх частка дорівнює 8. Знайдіть ці числа...
1 - Сума трьох натуральних чиселі дорівнює 825. Знайдіть ці числа, якщо перше...
2 - Одне із чисел у 7 разів менше від іншого. Знайдіть ці числа, якщо їх сума...
1 - Два автомобілі виїхали одночасно назустріч один одному із двох пунктів, відстань...
1 - Учень помножив деяке число окремо на 8 і на 12. Потім додав знайдені добутки...
1 - На трьох полицях стоять 96 книг. На другій полиці книг у 3 рази більше, ніж...
2 - Турист пройшов за чотири дні 92 км, причому кожного дня він проходив на 2...
2 - Основа рівнобедреного трикутника на 10 см менша від бічної сторони, а його...
3
Пошаговое объяснение:
Это сложная функция. Берем производную сперва от в степени, потом умножаем последовательно на производные вложенных функций: арктангенса, корня, квадрата:
в степени, потом умножаем последовательно на производные вложенных функций: арктангенса, корня, квадрата:
Производная сложной функции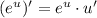 .
.