Впараллелограмме abcd точки p и q расположены на сторонах bc и ad так, что bp = bq. докажите, что четырехугольник apcq – параллелограмм.
Другие вопросы по теме Математика
Популярные вопросы
- Велосипед движется с постоянной скоростью 10 м/с, радиус его колеса...
2 - Замените косвенную речь прямой. 1.я позвонил моему другу, студента...
3 - Курица за месяц снесла 23 яйца,а индейка -на 11 яиц меньше.4 индюшачьих...
2 - Даны две последовательности целых чисел: a1, a2, a8 и b1, b2, b8....
3 - Комедия недоросль как автор относится к своим героям?...
3 - Спишите, раскрывая скобки. купле(н, нн)ый билет, лишё(н, нн)ый голоса,...
3 - Скласти спонукальне речення зі словом - хліб. позначити в цьому слові...
1 - Наппишите граммаиическую основу это художник много веков назад нарисовал...
1 - Три фирмы продали 236 компьютеров. 2-на 10%больше чем 1,3-на 100 шт....
3 - Эссе по теме станционный смотритель...
1
ABCD - параллелограмм, его диагонали точкой пересечения делятся пополам, т.е.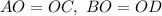 . По условию, BP = BQ, т.е., точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка, значит BO - высота, медиана и биссектриса равнобедренного треугольника
. По условию, BP = BQ, т.е., точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка, значит BO - высота, медиана и биссектриса равнобедренного треугольника 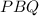 , тогда
, тогда 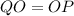 . А так как в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то четырехугольник
. А так как в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то четырехугольник 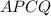 — параллелограмм.
— параллелограмм.