1. Математика
  2. Вдекартовой системе координат

Вдекартовой системе координат даны точки а(6; 3) и b(2; 4). точка с такова, что ос=оа-оb. найдите площадь треугольника аbc

Lika1639 Lika1639    2   23.08.2019 02:20    0

Ответы
tolyupa2000 tolyupa2000  05.10.2020 13:45

A (6; 3); B (2; 4)

Так как точка О имеет координаты (0; 0), то координаты векторов ОА и ОВ равны координатам точек А и В соответственно.

\vec {OA}(6;3); \vec {OB}(2,4)


\vec {OC}=\vec {OA}-\vec {OB}=(6-2;3-4)=(4;-1)

⇒ точка С имеет координаты (4; -1)


Площадь треугольника АВС можно вычислить как разность площади прямоугольника BMPN и угловых прямоугольных треугольников.

S_{ABC}=S_{BMPN}-S_{BNC}-S_{APC}-S_{AMB}=\\ \\ =5*4-\frac{5*2}{2} -\frac{4*2}{2} -\frac{4*1}{2} =20-5-4-2=9


ответ: С(4; -1);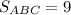 S_{ABC}=9 (кв.ед.)


Вдекартовой системе координат даны точки а(6; 3) и b(2; 4). точка с такова, что ос=оа-оb. найдите пл
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
tata479 tata479  07.07.2019 18:50
Сахарный песок упакован в пакеты по 3 кг сварили брусничное и земляничное варенье для варки брусничного варенья израсходовали 120 кг сахара,а для земляничного варенья 90 кг сахара...
SoniaSS09 SoniaSS09  07.07.2019 18:50
1м2дм+7м7дм-56дм= 8дм2см-44см2дм5см=...
arinakovtik arinakovtik  07.07.2019 18:50
Даны числа-64; -50; -20; -1.8; -0.75; 0.5; 15; 20; 28.изобразите промежуток и запишите,какие из этихчисел ему принадлежат: а)-0.75; 0.5 б)-1.8; 15в)-64; -20г)9; 28...
igor4321tryutr igor4321tryutr  07.07.2019 18:50
Первым,кто доказал,что кит-это не рыба,а зверь,был джон рей,а произошло это в 1693 году.несколько лет назад мы отметили юбилей этого события. какой? напишите решение...
7846854542 7846854542  07.07.2019 18:50
Известно что х*у=12. чем равно значение выражения: а)х*(у*5) б)(х*2)*у образец. х*(у*7)=(х*у)*7=12*7=84...
Сашок311 Сашок311  07.07.2019 18:50
Площадь криволинейной трапеции ограниченный линиями y=x^2 y=-x^2+8...
died267 died267  07.07.2019 18:50
Составь истеные равенства из велечин: 6мин; 20см; 1\2м; 20мин; 1\3ч; 5дм; 1\5 м; 1\4м; 25мин; 25см; 360с....
Аврoра Аврoра  07.07.2019 18:50
Удевочки было 150руб,90 она потратила на карандаши,40 на тетради.сколько денег осталось у девочки...
ufvsjfhgdgkhdvj ufvsjfhgdgkhdvj  07.07.2019 18:50
Условия применения методовв психолого-педагогических иследованиях нужно !...
6ytq3j5uhGBQ 6ytq3j5uhGBQ  07.07.2019 18:50
Впрямоугольнике длина длинее ширины на 13 см. площадь равна 140см2.как найти периметр?...

Популярные вопросы