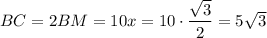Точка D - середина стороны AB, точка M - середина стороны BC треугольника ABC. Высота AH пересекает отрезок DM в точке K так, что DK=2KM . Найдите длину стороны BC, если AB=7 и AC=8.
Другие вопросы по теме Математика
Популярные вопросы
- Из-за чего петра гринёва посадили в тюрьму...
2 - Какие главные свойства персонажей выражены фонвизиным через фамилии...
3 - Что такое вес тела сила притяжения и как они связаны между собой?...
3 - Синтаксический разбор этого предложения обрывистый берег вест оброс...
3 - Найдите периметр трапеции стороны которой равны 4 см 6 см 4 см...
1 - Составить слово со словами i, але, а...
2 - Переведите текст на казахский . в доме находится шестеро человек....
1 - Как звали жителей нидерландов боровшихся с испанией?...
3 - Прочитайте отрывки из стих творения а.яшкина《 родные слова 》.почему...
3 - Сочинение по конфликтам “мещанин во дворянстве “...
3
Поскольку точки D и M соединяют отрезок середин AB и BC соответственно, то DM — средняя линия треугольника ABC.
По теореме Менелая:
Пусть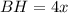 и
и 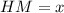 , тогда
, тогда 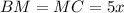 .
.
По теореме Пифагора из прямоугольных тр-ков ABH и AHC
От первого равенства отнимем второе, получим
Получаем