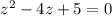Составьте квадратное уравнение с действительными коэффициентами, если известен один из его корней z1=2+i
Другие вопросы по теме Математика
Популярные вопросы
- Скорость катера против течения реки равна 17,8 км/ч, а собственная...
2 - Можете пожайлусто Решите систему неравенств!...
3 - Для приготовления фарфора смешивают белую глину, песок и гипс в...
2 - На теплоходе находиться 330 чел ,на яхте в 2 раза больше. Сколько...
2 - Правильный ответ написать(из предложенных выделенных слов)...
1 - Написати синкан про Івана Грозного...
2 - Выпишите местоимение,произведите морфологический разбор Люди ходят...
3 - Вычисли столбиком.проверь вычисления.103•5,;307•2;636:6;436:4;104•6;105•4;742:7;915:3...
2 - О каком человеке говорится в пословице от слова до дела сто перегонов...
1 - вариант. В ряду чисел 3, 8, 11, , 98,20, 28 пропущено одно число....
3
Нам требуется составить квадратное уравнение вида
Где a, b и c - действительные числа
Допустим мы составляем приведенное уравнение (a=1).
Тогда по теореме Виета
Для того, чтобы коэффициент c был действительным, мы можем принять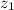 за сопряженное с
за сопряженное с 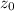 , т.е.
, т.е. 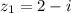 .
.
Логично, что для того, чтобы коэффициент b был действительным, требуется чтобы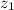 содержал комплексную часть, равную
содержал комплексную часть, равную 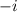 . Данное условие у нас уже соблюдается.
. Данное условие у нас уже соблюдается.
Теперь мы можем составить уравнение:
Проверка:
ответ: