1. Математика
  2. Сколько существует целых

Сколько существует целых значений a, при которых неравенство дальше во вложении


Сколько существует целых значений a, при которых неравенство дальше во вложении

    2   01.02.2022 10:11    0

Ответы
kamila0774 kamila0774  01.02.2022 10:20

0; 1; 2

Пошаговое объяснение:

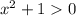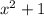Так как  x^2 + 1 0  для любого x, то можно умножить все части неравенства на  x^2 + 1, при этом сохранив знаки.

Получим  

-x^2 - 1 < ax^2 + x + 2 < 3x^2 + 3

Рассмотрим первое неравенство

1) \ ax^2 + x + 2 -x^2 - 1

(a + 1)x^2 + x + 3 0

Данному неравенству соответствует парабола

y = (a + 1)x^2 + x + 3

Для того, чтобы для всех x значения параболы были положительны, необходимо и достаточно выполнение двух условий:

а) Ветви параболы должны быть направлены вверх, то есть

a + 1 0 \Rightarrow a -1

б) Парабола не должна пересекать ось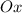 Ox (у неё не должно быть корней), то есть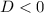 D < 0

D = 1 - 12(a + 1) \Rightarrow 1 - 12(a + 1) < 0

12a -11 \Rightarrow a -\dfrac{11}{12}

Из приведённых условий

\begin{cases} a -1 \\a -\dfrac{11}{12}\end{cases} \Rightarrow a -\dfrac{11}{12}

Рассмотрим второе неравенство

2) \ ax^2 + x + 2 < 3x^2 + 3

(a - 3)x^2 + x - 1 < 0

Данному неравенству соответствует парабола

y = (a - 3)x^2 + x - 1

Для того, чтобы для всех x значения параболы были отрицательны, необходимо и достаточно выполнение двух условий:

а) Ветви параболы должны быть направлены вниз, то есть

a - 3 < 0 \Rightarrow a < 3

б) Парабола не должна пересекать ось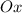 Ox (у неё не должно быть корней), то есть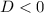 D < 0

D = 1 + 4(a - 3) \Rightarrow 1 + 4(a - 3) < 0

4a < 11 \Rightarrow a < \dfrac{11}{4}

Из приведённых условий

\begin{cases} a < 3 \\a < \dfrac{11}{4}\end{cases} \Rightarrow a < \dfrac{11}{4}

В итоге для двойного неравенства

\begin{cases} a -\dfrac{11}{12} \\ \\a < \dfrac{11}{4}\end{cases} \Rightarrow -\dfrac{11}{12} < a < \dfrac{11}{4}

В данном промежутке лежат следующие целые значения a:

a = 0, \ a = 1, \ a = 2


Сколько существует целых значений a, при которых неравенство дальше во вложении
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
marta894 marta894  09.08.2019 18:20
На рисунке на клетчатой бумаге с клетками одинаковых размеров изображены закрашенные фигуры,площади которых превосходят площадь одной клетки га фигуре 1 в 2 раза,на фигуре 2...
Marksensei Marksensei  09.08.2019 18:20
Сравните значения выражений1) (4-6)×5? (20×4)÷2= 2) 32÷(12-3-÷2)=...
svetlanaastahov svetlanaastahov  09.08.2019 18:20
Номер 2. запишите в виде бесконечное переодической дроби одиннадцать пятнадцатых...
inber657205 inber657205  09.08.2019 18:20
Т. к. точки a, b, c не лежат на одной прямой, то по аксиоме 1( через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом единственная) через них проходит...
лорею лорею  09.08.2019 18:20
Существует ли треугольник со сторонами 2,6,9?...
myyllaas myyllaas  09.08.2019 18:20
Сова болотная в 2 раза короче серого журавля.найдите длину каждого,если сумма длин журавля и совы равна 150см...
Со2006нь Со2006нь  09.08.2019 18:20
Вэтом мы будем исследовать и сравнивать некоторые свойства красок акварель и гуашь. леонардо....
Воробушка32 Воробушка32  09.08.2019 18:20
Не меняя порядка чисел, поставь знаки +, - , ×, ÷. так чтобы получилось 5,41, 54,168. 1 2 3 4 5=5 1 2 3 4 5=41 1 2 3 4 5=54 1 2 3 4 5=168...
Dezzy12 Dezzy12  09.08.2019 18:20
Вфутбольном турнире 6 команд сыграли между собой 2 тура — каждая кома н да сыграла с двумя разными . обязательно ли найдутся три команды, не сыгравшие пока между собой?...
Arigato99 Arigato99  09.08.2019 18:20
Слишком много поворов портят бульон подходящия пословица...

Популярные вопросы