((sin2x)/y + x)dx + (y - (sinx)^2/(y^2))dy =0

решить уравнения в полных дифференциалах

Ответы

Semykina2003 17.08.2020 06:28

$\left(\dfrac{\sin 2x}{y}+x\right)dx+\left(y-\dfrac{\sin^2x}{y^2}\right)dy=0\\ \\ \underbrace{\left(\dfrac{\sin 2x}{y}+x\right)}_{M(x,y)}dx+\underbrace{\left(y-\dfrac{1-\cos 2x}{2y^2}\right)}_{N(x;y)}dy=0$

Уравнение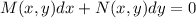 M(x,y)dx+N(x,y)dy=0 является в полных дифференциалах, поскольку выполняется равенство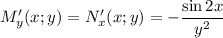 $M'_y(x;y)=N'_x(x;y)=-\dfrac{\sin 2x}{y^2}$

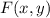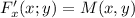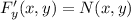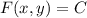Если функция F(x,y) удовлетворяет F'_x(x;y)=M(x,y) и F'_y(x,y)=N(x,y) , то F(x,y)=C - решение уравнения

Интегрируем функции F по переменной х

$F(x,y)=\displaystyle \int M(x,y)dx=\int\left(\dfrac{\sin 2x}{y}+x\right)dx=\dfrac{x^2}{2}-\dfrac{\cos 2x}{2y}+C(y)$

Далее дифференцируем по у

$F'_y(x,y)=\left(\dfrac{x^2}{2}-\dfrac{\cos 2x}{2y}+C(y)\right)'_y=\dfrac{\cos 2x}{2y^2}+C'(y)$

Действительно,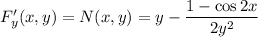 $F'_y(x,y)=N(x,y)=y-\dfrac{1-\cos 2x}{2y^2}$ . Отсюда $C'(y)=y-\dfrac{1}{2y^2}~~~\Rightarrow~~~ C(y)=\dfrac{y^2}{2}+\dfrac{1}{2y}$

Общий интеграл

$\dfrac{y^2}{2}+\dfrac{1}{2y}-\dfrac{\cos 2x}{2y}+\dfrac{x^2}{2}=C$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

fatowka84 15.12.2020 11:31

я не знаю как это делать ...

eerihovp08oqz 15.12.2020 11:30

При a=1,25 подробное решение...

katyakot2299 15.12.2020 11:30

№1. Раскройте скобки. 1) 2,5(4а-2)-0,5(3а+9) 2) 2/3 (9d+6m-a)-4/7(7d-m+7/16 a) 3) -6(x+2y)+1/5 (10x-125y) №2. Найдите значение выражения 26a-12(a+b), если 7a-6b= 1/2 №3. Найдите...

hramkova1983 15.12.2020 11:30

желательно развёрнутый ответ...

адекс3 15.12.2020 11:30

Решите уровнение (у-4)(у+4)=2(5у+4)...

Iaro 15.12.2020 11:29

На рисунке изображена окружность радиус которой равен 2 см.Построй 12 окружностей с центром и отмеченными точками радиусом 1 см....

тимур624 15.12.2020 11:29

желательно развёрнутый ответ...

ggwp49 15.12.2020 11:28

Найдите sin, tg, ctg если cos =-2/3...

kasatka0556 15.12.2020 11:28

№1 Дано: Е(4;12), F(-4;-10), G(-2;6), H(4;-2) Найти: а) координаты векторов EF, GH б) длину вектора FG в) координаты точки О – середины EF, координаты точки W – середины GH...

ХарламоваяАня 15.12.2020 11:27

[ ] Постройте четырехугольник, гомотетичный четырехугольника АВСД, если даны центр гомотетии О и её коэффициент к= - 1/2...

((sin2x)/y + x)dx + (y - (sinx)^2/(y^2))dy =0 решить уравнения в полных дифференциалах

Популярные вопросы

((sin2x)/y + x)dx + (y - (sinx)^2/(y^2))dy =0

решить уравнения в полных дифференциалах