Решите уравнение ( sin x + cos x)^2= 1-sin x * cos x
)))
Другие вопросы по теме Математика
Популярные вопросы
- Составить 4 предложения со словами мені , менен , менде заранее...
2 - Докажите что если две наклонные проведенные из данной точки к данной прямой имеют...
1 - Решить . при напряжении на концах проводника 2 в сила тока в нём 0,8 а. каково напряжение...
1 - Запиши цифры в порядке убывания 8,5 в 8,16 в 8,4 в 8,49 в 8,05 и 8,61...
3 - Слово ,,голова .подберите 5-6 синонимов.к этому слову. разговорные,книжные,нейтральные...
1 - Скакими понятиями вы познокомились в...
3 - Напишите сочинение о том как вы понимаете высказывание ни один народ в мире не одарен...
1 - Купили однакову кількість підручників і словників.за всі підручники зп аплатили360...
3 - На коробке с канфетамм надпись: 0,8 кг 384 тг.найдите цену 1 кг...
3 - Сочинение на тему кем я хочу стать (хочу быть боксёром)....
3
Пошаговое объяснение:
( sin(x) + cos(x))^2 = 1-sin(x) * cos(x)
разложим уравнение используя (a+b)^ = a^2-ab+b^2
sin(x)^2+2sin(x)cos(x)+cos(x)^2 = 1-sin x * cos x
упрощаем выражение, используя sin(t)^2+cos(t)^2=1
1+2sin(x)cos(x) = 1-sin(x)cos(x)
упрощаем выражение, используя 2sin(t)cos(t)=sin(2t)
1+sin(2x) = 1-sin(x)cos(x)
сократим равные члены в обеих частях уравнения
sin(2x) = -sin(x)cos(x)
переместив выражение в левую часть, прибавляем противоположное ему выражение к обеим частям
sin(2x)+sin(x)cos(x) = -sin(x)cos(x)+sin(x)cos(x)
сумма двух противоположных чисел равна 0
sin(2x)+sin(x)cos(x) = 0
используем sin(2t) = 2sin(t)cos(t)
2sin(x)cos(x)+sin(x)cos(x) = 0
приводим подобные члены
3sin(x)cos(x) = 0
делим обе стороны на 3
sin(x)cos(x) = 0
если произведение равно 0, то как минимум один из множителей равен 0
sin(x) = 0
cos(x) = 0
решаем уравнение относительно х
x = kπ, k∈Z
x =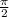 +kπ, k∈Z
+kπ, k∈Z
Объединяем
x =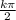 , k∈Z
, k∈Z