Решите уравнение ( с производной)
Другие вопросы по теме Математика
Популярные вопросы
- Бунин Цифры таблица поступок Жени реакция дяди...
3 - Найдите корни уравнения. Укажите наибольший отрицательный корень....
2 - Эссе моё хобби: готовить и рисовать ...
2 - Может ли Соня Мармеладова «воскресить» Лужина?...
2 - Нужна Сделайте следующие предложения во...
1 - Як наш клас готовит контент для своего блогу...
2 - Синтаксический разбор предложения отец отличный мастер...
2 - «Внутренняя политика России в начале XXI в.: основные направления и результаты»...
2 - Инфознайка 2020 5-7 класс, решите очень нужно....
3 - 1. В равнобедренном треугольнике АВС АВ=ВС, ВЕ - биссектриса, точка Н лежит...
3
x =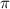 +2*
+2*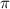 *n; x = ±
*n; x = ±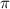 /3 + 2*
/3 + 2*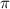 *n
*n
Пошаговое объяснение:
f'(x) = (sin x)' + 1/2* (sin 2x)' = 0
cos x + 1/2*cos 2x * 2 = 0
cos x + cos 2x = 0
cos x + 2*(cos x)^2 - 1 = 0
Введемо заміну t = cos x і отримаємо квадратне рівняння
2*t^2 + t - 1 = 0
D = 1 +4*2 = 9
t1 = (-1 - 3)/4 = -1 t2 = (-1 + 3)/4 = 0,5
cos x = -1 cos x = 0,5
x =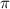 +2*
+2*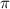 *n x = ± arccos(0,5) + 2*
*n x = ± arccos(0,5) + 2*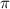 *n = ±
*n = ±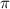 /3 + 2*
/3 + 2*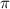 *n
*n