Решите уравнение (ответ отмечен, нужно решение)

Другие вопросы по теме Математика
Популярные вопросы
- Миниатюра с фрозиологизмом любым ...
2 - Впервом доме 24 двухкомнатные и 48 трехкомнатные квартир, во втором – 16 двухкомнатных...
2 - Самостійна робота – запис есе додатковий матеріал: 1. серце 2. добре, велике...
3 - Используя формулу квадрата суммы или квадрата разности двух выражений вычислите...
3 - 5§ государство огузов(lх-середина хl вв)конспект. ...
1 - Найти значение числового выражения 47^2-2*47*27*27^2...
3 - Краткое сообщение об исследованиях гор южной сибири (нужно написать про учёных,...
1 - 4,06×0,0058+3,3044895-(0,7584: 2,37+0,0003÷8)=? решить...
2 - На доске 6×6 стоит 6 ладей, как показано на рисунке.за один ход разрешается...
1 - Какое прилагательное в тексте является эпитетом? глухой лес лесная мышь чёрные...
3
x=-2
Пошаговое объяснение:
Заметим, что левая функция всегда неотрицательная, а у правой функции в неотрицательную область попаает только одна ветвь параболы. (т.к.![\[t \ge 0\]](/tpl/images/1361/5392/8d27e.png) )
)
Значит у функций будет одно пересечение(т.е. одно решение), которое не сложно подобрать при t=4.
ответ:
Пошаговое объяснение:
Пусть:
Тогда уравнение принимает вид:
Заметим, что если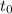 корень уравнения
корень уравнения 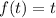 , то он и корень уравнения:
, то он и корень уравнения:
Найдем все такие корни:
Заметим, что функция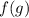 - монотонно возрастает.
- монотонно возрастает.
Предположим, что в уравнении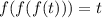 существует корень
существует корень 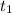 , такой, что
, такой, что 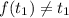
Рассмотрим случай: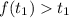 .
.
Поскольку,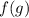 - монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство:
- монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: 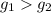 , то верно и данное неравенство:
, то верно и данное неравенство: 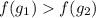
Из данного утверждения следует, что :
Но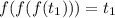 , то есть мы пришли к противоречию.
, то есть мы пришли к противоречию.
Аналогично показывается невозможность утверждения для случая