Решите , если нетрудно распишите подробно каждое ваше действие, и если не трудно напишите формулы какие используете...
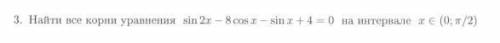
Другие вопросы по теме Математика
Популярные вопросы
- Найдите объём и площади полной и боковой поверхности прямоугольного параллелепипеда,если...
2 - Визначте период обертання колеса автомобиля якщо його швидкисть v=15м\с...
2 - Пример реакций с выделением тепла. пример с поглощением тепла....
2 - Движение материальной точки задано уравнением х=2+2т-0.5т^2. напишите...
2 - На какой из слитков золота действует меньшая сила тяжести и во сколько...
1 - Сепаратистские движения в чечне в начале 90-х?...
3 - Из перечисленных признаков найдите характерные для класса однодольные...
1 - При сжигании 2л ацетилена выделилось 116,0 кдж теплоты. найдите тепловой...
2 - Вырастили две тыквы одна весом 26 кг а другая 22 кг. на сколько кг первая...
3 - Определить плотность стекла , из которого сделан куб массой m=790 г ,...
3
ответ: х = π/3 .
Пошаговое объяснение:
3 . sin2x - 8cosx - sinx + 4 = 0 ; хЄ ( 0 ; π/2 ) ;
2sinxcosx - 8cosx - sinx + 4 = 0 ;
2cosx( sinx - 4 ) - ( sinx - 4 ) = 0 ;
( 2cosx - 1 )( sinx - 4 ) = 0 ;
2cosx - 1 = 0 ; або sinx - 4 = 0 ;
cosx = 1/2 ; sinx = 4 ;
x = ± π/3 + 2πn , nЄ Z ; x Є∅ .
Із знайденої серії коренів тільки х = π/3 Є ( 0 ; π/2 ) .