решить второй замечательный предел
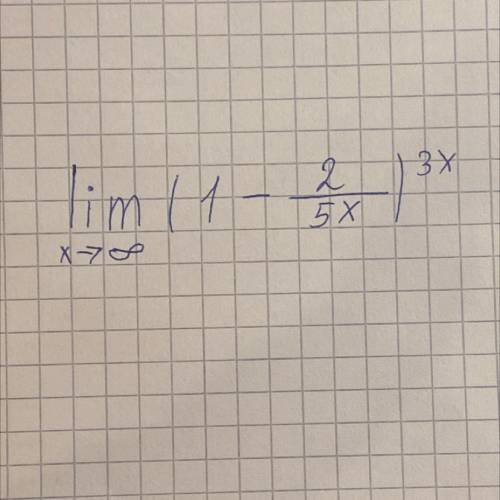
Другие вопросы по теме Математика
Популярные вопросы
- Одна сторона прямоугольника на 2 см больше другой. Периметр равен 36 см....
2 - Оформить таблицу Ивана IV «Дата/ реформа/ содержание»....
3 - Автомобиль начинает движение из состояния покоя с ускорением 4 м/с2. За которую...
1 - 1.3. Император Византийской империи объединял политические и ………………функции....
3 - Те,кто хорошо знают английский! >...
3 - Два джигита соревновались: чей конь придёт к финишу последним. Однако дело...
3 - Образуйте от глаголов действительные причастия настоящего времени ,а затем...
3 - проверьте, верна ли данная пропорция, используя основное свойство пропорции:...
3 - Какова тема вышеизложенного монолога Чацкого? А)Обличение общества за следование...
2 - Установите последовательность стадий развития папоротника,...
1
\begin{gathered}lim_{x- > \infty }(1 - \frac{2}{5x} ) ^{3x} \\ \\ lim_{x- > \infty }(1 + \frac{1}{x} ) ^{x} = e \\ \\ lim_{x- > \infty }(1 + ( - \frac{2}{5x} )) ^{ - \frac{5x}{2} \times( - \frac{6}{5} ) } = \\ = {e}^{ - \frac{6}{5} } = \frac{1}{ \sqrt[5]{ {e}^{6} } } \end{gathered}
lim
x−>∞
(1−
5x
2
)
3x
lim
x−>∞
(1+
x
1
)
x
=e
lim
x−>∞
(1+(−
5x
2
))
−
2
5x
×(−
5
6
)
=
=e
−
5
6
=
5
e
6
1