1. Математика
  2. Решить. вроде как надо вычислить

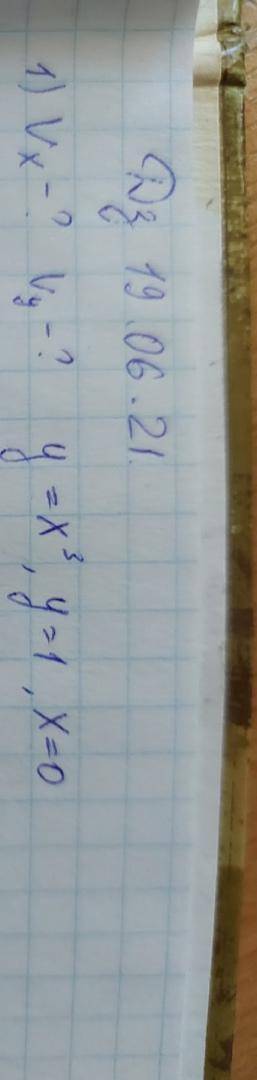
Решить. вроде как надо вычислить объём тела вращения по оси ОХ и ОУ
нарисовать рисунок


Решить. вроде как надо вычислить объём тела вращения по оси ОХ и ОУ нарисовать рисунок

97shadesofblue 97shadesofblue    3   06.07.2021 13:45    0

Ответы
dadasova dadasova  05.08.2021 14:22

Пошаговое объяснение:

формула для вычисления объема тела вращения вокруг оси ОХ

\displaystyle V_{OX}=\pi \int\limits^a_b {y^2(x)} \, dx\qquad \boldsymbol {(1)}

формула для вычисления объема тела вращения вокруг оси ОY

\displaystyle V_{OY}=\pi \int\limits^a_b {x^2(y)} \, dx \qquad \boldsymbol {(2)}

в нашем случае

\displaystyle y=x^3\\x=\sqrt[3]{y}

из графика видим, что пределы интегрирования в обоих случаях одинаковы

считаем

1. вокруг оси ОХ у нас область не прилегает к оси ОХ, поэтому будет объем Vох = V₁ - V₂, где

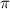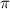V₁ - объем цилиндра (R=1, h=1)который равен \displaystyle \pi (V= \displaystyle \piR²h) и объем фигуры (вроде воронки), которую считаем по формуле (1), поэтому наш объем считаем

\displaystyle V_{OX}=\pi -\pi \int\limits^1_0 {(x^3)^2} \, dx =\pi \frac{1}{x^7} \bigg |_0^1=\pi -\frac{\pi}{7}=\frac{6\pi }{7}

2. вокруг оси ОУ у нас дырки нет, область полностью прилегает к оси ОУ, поэтому просто считаем по формуле (2)

\displaystyle V_{OY}=\pi \int\limits^1_0 {(\sqrt[3]{y} )^2} \, dy =\pi \int\limits^1_0 {y^{2/3}} \, dy =\pi \frac{3y^{5/3}}{5} \bigg |_0^1=\frac{3\pi}{5}

на схеме

красная штриховка - "воронка"

синяя -  наша фигура


Решить. вроде как надо вычислить объём тела вращения по оси ОХ и ОУ нарисовать рисунок
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
MINdana MINdana  30.10.2020 10:38
РЕБЯТА У МЕНЯ СОЧ Задания суммативного оценивания за 1 четверть. 6 класс. 1. Задана пропорции найдите х : а) 12,4/х=1,2/0,6 б) х : 2,8 = 5 : 7 [2] 2. Расстояние между...
vfeukb59Pavek vfeukb59Pavek  30.10.2020 10:38
в программе по геометрии 40 билетов из которых шесть билетов на тему подобие тося случайно выбрала билет какова вероятность того что в билете есть вопрос о подобии...
oiopiha oiopiha  30.10.2020 10:38
Реши уравнения полностью с проверкой...
ромакравчук12 ромакравчук12  30.10.2020 10:38
Решите уравнение и выполните проверку:...
POULINACAT POULINACAT  30.10.2020 10:38
Решите графически уравнение...
Вовчик256 Вовчик256  30.10.2020 10:38
1. Скільки існує десятицифрових чисел, в записі яких є хоча б дві однакові цифри? 2. Маємо множину C, яка складається з n елементів. Скількома можна вибрати в C дві...
stregubkin stregubkin  30.10.2020 10:38
Найти уравнение медианы, высоты треугольника АВС проведенных из точки А, средней линии, параллельной АВ, если известно: А(1;3), В(0;5), С(-2;-1). Вычислить длину найденной...
Джейн2005 Джейн2005  23.09.2020 12:16
Найдите значение выражения : 13:4 ,74:15​...
lolkek12398 lolkek12398  23.09.2020 12:15
2x-3приx=4;0;-3 нувотпмтб со чит, ьс о. р о​...
Діанагрeк Діанагрeк  23.09.2020 12:15
решить! Даю очень много: (​...

Популярные вопросы