1. Математика
  2. Решить уравнение : tg3x=√3/3

Решить уравнение : tg3x=√3/3 решить уравнение : 2cos²(x-)+3sin(+x)+=0 (формула )

Topxic Topxic    1   04.10.2019 03:10    2

Ответы
Анонимка00 Анонимка00  09.10.2020 18:42

Пошаговое объяснение:

tg3x=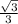 \frac{\sqrt{3} }{3}

3x=arctg  \frac{\pi }{6} +\pi n , n∈z

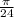x = \frac{\pi }{24} + \frac{\pi n }{3} , n∈z


2cos² (x-\pi) + 3sin(\pi+x)=0

2-2sin²x - 3sinx = 0

2sin²x + 3sinx -2=0

2t² + 3t - 2 = 0

D = 9 + 16 = 25

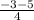x₁ = \frac{-3 + 5 }{4} = \frac{1}{2}

x₂ = \frac{-3 - 5 }{4} = -2

x₁ = \frac{1}{2}

x = (-1)ⁿ arcsin \frac{\pi }{6} + \pi n , n∈z

x₂ = -2

∅  

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Настечок Настечок  16.04.2021 10:32
Задание 1. По заданным значениям переменной у, найдите соответствующее значение аргумента х, если у = -5,6х + 10 и у = -12,4 .​...
irinalove2 irinalove2  16.04.2021 10:33
-2(1,5х – 2,6у) + 3(-3,7х +2,9у)= ​...
efimovvvilyha efimovvvilyha  16.04.2021 10:33
1156. Автотуристы в первый день проехали 36%, 50 второй день 39% намеченного пути, а в третий день OCTasnecs 180 км. Сколько всего километров проехали автотуристы? сделайте...
сонечка3332002 сонечка3332002  16.04.2021 10:33
В першому магазині в 4 раза менше роботів ніж у другому. Після того як в перший магазин завезли ше 35 роботів, а в другому продали 25 роботів, їх в магазинах стало порівну....
munisa333 munisa333  16.04.2021 10:33
Шифер должен проехет 350 км .Он ужепроехал0,7 намеченного пути .Сколька километров ему осталось проехать​...
ksyusa41 ksyusa41  16.04.2021 10:33
При каком значении числа a уравнение 5ax = 14 – x имеет корень, равный 4?...
Yuran3 Yuran3  16.04.2021 10:33
Знайти число b якщо а =24,2 а середнє арифметичне чисел а і b дорівнює 36...
alaska122 alaska122  16.04.2021 10:33
Дослідити функцію за до похідної та побудувати її графік(повне дослідження)...
alina1427 alina1427  16.04.2021 10:34
Дано: AD, AB, BC - касательные к окружности, D, M, C - касательные, KA = B = 60 , BM = x. Напишите выражение, выражающее длину периметра треугольника DMC. ​...
alicianovikova alicianovikova  16.04.2021 10:34
！ у меня к.р. с математики ЕСЛИ БУДЕТЕ ПИСАТЬ ТУПУЮ ФИГНЮ ТОЛЬКО ЧТОБЫ ЗАРАБОТАТЬ БАН НА ВСЕГДА！​...

Популярные вопросы