решить тригонометрические уравнения.
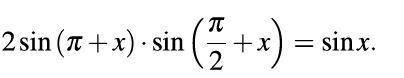

Другие вопросы по теме Математика
Популярные вопросы
- Кто знает известных людей череповца? нужен ответ!...
1 - Очём составляет задуматься рассказ уроки французского ?...
3 - Вкаком из перечисленных регионов россии средняя плотность населения наибольшая?...
1 - Ситуацию на пословицу что посеешь то и пожнешь на ты...
1 - Complete the sentences. use ‘ll or won t. amy s brother is thirteen. be fourteen...
3 - Сообщение п биологии о лебеде на пол страницы...
2 - Ширину прямоугольника увеличили на 20 см а длину уменьшили на 20% площадь нового...
1 - 1. у каких представителей высших растений корневая система представлена ? а) мхи...
2 - Используя не менее двух предложений, опишите ситуацию, в которой уместно будет...
3 - Влияние биологических и социальных факторов на ход антропогенеза...
2
1)
2)
Пошаговое объяснение:
1)
Преобразуем:
Отсюда:
Мы получили 2 простых триг. уравнения:
1)
Решим оба получившихся уравнения:
ответ
2) - см. на приложенном фото
ответ
Решение задания прилагаю