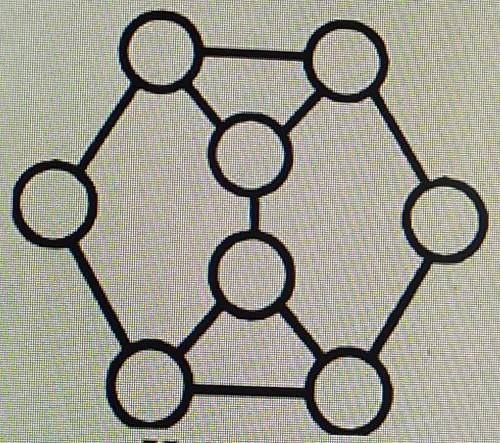
Расставьте кружки числа от 2 до 9( без повторений) так, чтобы никакое число не делило бы нацело ни одного из своих соседей​

Чтобы расставить кружки чисел от 2 до 9 так, чтобы никакое число не делило бы нацело ни одного из своих соседей, мы должны следовать нескольким правилам.

Правило 1: Числа 2 и 3 должны быть соседними. Это связано с тем, что у нас есть только одно четное число, 2, и одно число с единичной цифрой, 3. Это позволяет найти наилучшее расположение для них, чтобы избежать деления нацело.

Правило 2: Число 4 должно быть соседним с 2 или 3. Если оно будет соседствовать с 5, то 2 или 3 должны будут быть соседними с 4, и это противоречит первому правилу.

Правило 3: Число 6 не может быть соседним с 3, так как 3 является простым числом, и оно имеет только два делителя: 1 и само себя.

Исходя из этих правил, рассмотрим следующие варианты расстановки:

Вариант 1:
3 - 4 - 2 - 5 - 7 - 8 - 6 - 9

Проверим, удовлетворяют ли эти числа всем правилам:

- 3 не делится ни на 4, ни на 2
- 4 не делится ни на 3, ни на 2
- 2 не делится ни на 3, ни на 5
- 5 не делится ни на 2, ни на 7
- 7 не делится ни на 5, ни на 8
- 8 не делится ни на 7, ни на 6
- 6 не делится ни на 9, ни на 8
- 9 не делится ни на 6, ни на 8

Вариант 1 удовлетворяет всем правилам, поэтому он является допустимым решением.

Вариант 2:
2 - 5 - 7 - 3 - 4 - 9 - 6 - 8

Проверим, удовлетворяют ли эти числа всем правилам:

- 2 не делится ни на 5, ни на 7
- 5 не делится ни на 2, ни на 7
- 7 не делится ни на 5, ни на 3
- 3 не делится ни на 7, ни на 4
- 4 не делится ни на 3, ни на 9
- 9 не делится ни на 4, ни на 6
- 6 не делится ни на 9, ни на 8
- 8 не делится ни на 6, ни на 9

Вариант 2 также удовлетворяет всем правилам, поэтому он также является допустимым решением.

Итак, мы можем выбрать любой из двух вариантов:

- 3 - 4 - 2 - 5 - 7 - 8 - 6 - 9
- 2 - 5 - 7 - 3 - 4 - 9 - 6 - 8