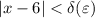Пользуясь определением доказать что функция f x непрерывна в точке a
f(x)=-5*x2-7, a=6
f(x)=5*x2+2, a=6
Другие вопросы по теме Математика
Популярные вопросы
- Охарактеризуйте андрия и остапа (тарас бульба). умоляю надо! заранее всем...
3 - За несколько часов автобус должен проехать 400 км. через 6 часов ему осталось...
2 - Купили 6 кг яблок и 9 кг груш. за всю покупку заплатили 222 рубля. сколько...
1 - Нужно написатьпро зимние изменения в природе. это нужно по окружающему...
3 - Вмагазин 64 кг винограда в 8 ящиках.к концу дня осталось 24 кг винограда....
3 - 1.кто был основателем томизма? 2.когда началась жакерия во франции? 3.куда...
1 - Билет в цирк для взрослого стоит 3000 рублей. стоимость билета для школьника...
1 - Каково было количество возможных событий, если после реализации одного...
3 - При движении тела вдоль оси х координата тела меняется по закону: х=300+30t-3t^2....
1 - От наречий качественно, высоко, строго, рано, тихо образуйте все возможные...
1
Функция f(x) непрерывна в точке a = 6, если
Это значит, что для положительных неравенство
неравенство 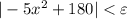 имеет решение
имеет решение 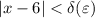
2)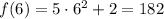
Функция f(x) непрерывна в точке a = 6, если
Это значит, что для положительных неравенство
неравенство 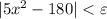 имеет решение
имеет решение