найти решение системы уравнений:
(x + 2)(y - 6) = 0
x^2 - xy - 12 = 0
Другие вопросы по теме Математика
Популярные вопросы
- Напишите своё мнение от каких факторов зависит индивидуальное здоровье...
1 - Реагируют ли соли с основными (например cuo+mgso4, zno+na2so4)...
3 - Надо определите кол-во корней уравнения 3sin8x=x^{3}...
3 - Сколько этапов на пути к писательству иван шмелев...
2 - 26 . , , решить этот пример. 5√x+3+x+3=6...
1 - Долгом и обязанностью каждого совершеннолетнего гражданина рф является: -участие...
1 - Перевести правила на , (не при переводчика): мои правила 1.я не против общения,...
2 - По чтении 2 класс стих в бурю придумать 5 вопросов...
2 - Сочинение на тему ,,как правильно выполнянь по языку. заранее ....
1 - Велосипедист проехал по асфальту 2 часа со скоростью 13 км в час и по грунтовой...
3
-2
Пошаговое объяснение:
для того чтобы найти У , надо подставить Х в
формулу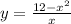 в ответе соответствующие пары
в ответе соответствующие пары