1. Математика
  2. Найти радиус сходимости и интервал

Найти радиус сходимости и интервал сходимости степенного ряда

сссс27 сссс27    2   17.03.2020 09:55    1

Ответы
3333100 3333100  11.10.2020 23:50

\sum\limits_{n=1}^\infty \dfrac{(x+1)^{2n}}{9}=\sum\limits_{n=1}^\infty a_n

\lim_{n\to\infty}\sqrt[n]{a_n}=\lim_{n\to\infty}\sqrt[n]{\dfrac{(x+1)^{2n}}{9}}=(x+1)^2

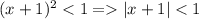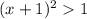Ряд сходится при (x+1)^2|x+1| и при (x+1)^21 расходится по признаку Коши.

Тогда радиус сходимости равен 1, а интервал получим из неравенства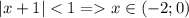 |x+1|x\in(-2;0)

ответ: 1; (-2;0)

____________________________

Степенной ряд имеет вид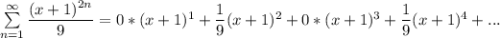 \sum\limits_{n=1}^\infty \dfrac{(x+1)^{2n}}{9}=0*(x+1)^1+\dfrac{1}{9}(x+1)^2+0*(x+1)^3+\dfrac{1}{9}(x+1)^4+...

Тогда последовательность коэффициентов степенного ряда разбивается на 2 подпоследовательности: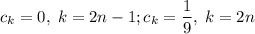 c_k=0,\; k=2n-1; c_k=\dfrac{1}{9},\; k=2n

Тогда используем формулу Коши-Адамара:

\dfrac{1}{R}=\overline{\lim\limits_{k\to\infty}}\sqrt[n]{|c_k|}=\max\{0, \lim\limits_{n\to\infty}\sqrt[2n]{\dfrac{1}{9}}\}=1=R=1=x\in(-2;0)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
alinakim3 alinakim3  13.04.2020 01:34
решить пример cos a - sin(-a) * ctg(- a)...
kisa93445 kisa93445  13.04.2020 01:34
Cos a - sin (-a) * ctg(- a)...
bezrodnyhartem2Arizi bezrodnyhartem2Arizi  13.04.2020 01:16
Сравни числа(задание учи.ру)V- неизвестный знак равенства( , , =)[ ] - сюда нужно вставить число √26+2 V 6 |-2√26+2-2 V 6-2 [ ] V [ ]...
makhnoliza makhnoliza  13.04.2020 01:16
1. Представь 0,125х2у21 в виде куба одночлена. 2. Неполный квадрат суммы одночленов t и 0,5 равен.. ​...
mailrujl mailrujl  13.04.2020 01:16
6.Ракета движется прямолинейно по закону x(t)=0,34е4t+21 (где х – расстояние от поверхности земли в метрах, t – время в секундах). С какой скоростью стартовала ракета?...
andreevochir20 andreevochir20  30.03.2020 21:31
АЛГЕБРА ІВ на пошті є три види конвертів, два види марок до них і чотири види а оздоровчих листівок, що вкладаються в ці конверти. скільки існує різних в оформлення одного...
80zumani 80zumani  30.03.2020 21:31
НАЙТИ ЗНАЧЕННЯ ВИРАЗУ 3х+у,якщо х=-3,у=-4...
Petrosyan31337 Petrosyan31337  30.03.2020 21:30
первое и второе задание) ​...
nikitamakarov3 nikitamakarov3  30.03.2020 21:30
подобрать правильный ответ к каждому примеру, на 1 скриншоте примеры, на 2 ответы...
merhanoooI merhanoooI  30.03.2020 21:30
Решите с дискримината 5x^2-9x-2=0 3x^2+11x+2=0...

Популярные вопросы