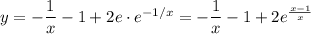Найти частное решение дифференциального уравнения:
Другие вопросы по теме Математика
Популярные вопросы
- Какое слово в предложениях соответствует по лекчическому значению...
1 - Значение пословицы к пиру пришлось, к слову молвилось!...
1 - Рая, сима и таня ели в саду фрукты. рая съела 10 слив и столько...
3 - Внекотором каталоге хранится файл .txt. в этом каталоге создали...
1 - Почему в предложении в государстве ромашек, у края, ставится запятая...
1 - *вычеркните лишнее* какие государства входили в монгольское государство,созданное...
1 - Примеры цветочных культур выращиваемые в дагестане...
1 - Выражение -2a(3a-b)-8b(4a+3b) при a=0.1, b=-0.2...
1 - Уровнение реакций позволяющих осуществить превращение ca- cah2...
3 - 1.напишите, кого испанцы называли недосожженные и почему? 2.напишите...
3
Перепишем данное дифференциальное уравнение в виде:
Умножив обе части уравнения на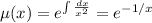 , мы получим
, мы получим
Интегрируем обе части уравнения
Решим интеграл стоящий справа уравнения отдельно
Получаем
Подставляя начальные условия, найдем константу C
Частное решение: