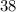Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=3x^3+2x-5 в его точке абсциой x=2
Другие вопросы по теме Математика
Популярные вопросы
- Мне нужно правило решение уравнения содержащие одну под знаком модуля...
3 - Укажите, к какому классу соединений принадлежит каждое из предложенных...
1 - Функций у=2х^, у=х/х-3, у=2х+5 выберите линейную. найдите для нее...
2 - Choose the correct synonym of : tied: a-joined b-twisted c-tried...
3 - Животные которые выполняют роль санитаров...
3 - Даны два числа: 23562 и 7839. определи старший разряд суммы этих...
2 - Вставьте в данных предложениях запяты где это надо! и объясните...
3 - С! заполни пропуски в уравнениях реакций,уравняй их и составь ионные...
3 - Ex 6. correct mistakes if it’s necessary. 1. on the photo i can...
3 - Представьте квадрат двучлена (c^3+8m^3)^2 в виде многочлена....
3
Подставляем 2 это и будет коэффициент
9*4+2=38
Воспользуемся тем, что угловой коэффициент, численно равен производной данной функции откуда получаем:
Получаем:
Где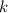 и есть данный угловой коэффициент, а
и есть данный угловой коэффициент, а 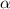 есть угол наклона касательной к графику функции в некоторой точке.
есть угол наклона касательной к графику функции в некоторой точке.
Вычислим значение углового коэффициента в точке, абсцисса которой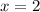
Получаем:
ответ: значение углового коэффициента в точке, абсцисса которой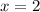 равен
равен