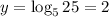Найдите наибольшее значение функции y = log5 (6x - x^2 + 16)
Другие вопросы по теме Математика
Популярные вопросы
- Причини зародження і особливості дисидентського руху в україні...
1 - Перепишіть, уставляю чи пропущенілітери. визначте особу, число...
1 - Уколи есть монеты по 2 рубя и по10 рублей.всего на сумму 108 рублей.монет...
2 - Все стихотворение это рассказ старого солдата о бородинском сражении...
1 - Дана одна цепочка днк. пользуясь принципов комплементарности,постройте...
3 - Делительная воронка применима для разделения смеси воды и: 1)сахара...
1 - Найти промежутки монотонности функции; понятно, что нужно найти...
2 - А. технология индустриального производства. б. машиностроение....
1 - Заполнить прочерки )температура воды в мировом океане изменяется...
2 - Смесь карбоната и сульфита кальция массой 34 г обработали раствором...
2
Если рассмотреть функцию под логарифмического выражения, то графиком функции квадратичной функции является парабола, ветви направлены вниз. Квадратичная функция достигает наибольшего значения в точке х=3, равно 25.
В данном случае, заданная функция достигает наибольшего значения в точке х=3, равное