Найдите частное решение уравнения
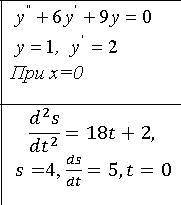
Другие вопросы по теме Математика
Популярные вопросы
- Найти общее и частное решение y -8y =0...
2 - В каком направлении произойдёт смещение равновесия при понижении давления систем:...
1 - Асқабақтың пайдасы қандай?...
2 - Объясните подробно решение уравнения, нужно упростить sin18cos18cos36 до (1/4)...
2 - Рассчитайте молярность раствора сильной кислоты НА, если известно значение...
3 - решить и обьяснить шаги решения)...
2 - Бұл мәтінге жоспар құру керек!...
3 - решить проблему в игре Oxygen not included...
1 - У какого элемента последний электрон, заполняющий атомные орбитали, имеет следующие...
3 - Transform the verb into the Past Indefinite Tense and make negative sentences...
2
ответ: а ) у = ( 1 + 5х )e⁻³ˣ ; б ) s( t ) = 3t³ + t² + 5t + 4 .
Пошаговое объяснение:
a ) y '' + 6y + 9y = 0 ; y(0) = 1 ; y '(0) = 2 ; x₀= 0 ;
характеристичне рівняння : k² + 6k + 9 = 0 ; ( k + 3 )² =0 ; k₁= k ₂ = - 3 .
y = ( C₁ + C₂x)e⁻³ˣ - загальний розв"язок диф . рівняння .
y '= C₂* e⁻³ˣ - 3(C₁ + C₂x )e⁻³ˣ ;
y( 0) = 1 = ( C₁ + 0*C₂)e⁻³°⁰ ; C₁ = 1 ;
y'( 0) = 2 = C₂*e⁻³°⁰ - 3( C₁ + C₂* 0)e⁻³°⁰ ; C₂ - 3C₁ = 2 ; C₂ =3C₁+2 =3*1+2 =5 ;
Отже , у = ( 1 + 5х )e⁻³ˣ - відповідь .
б ) d²s/dt² = 18t + 2 ; s(0) = 4 ; ds/dt = 5 при t = 0 .
Інтегруємо обидві частини рівності :
ds/dt = ∫ (18t + 2)dt = 9t² + 2t + C₁ ; ds/dt = 9t² + 2t + C₁ .
Інтегруємо ще один раз :
s( t ) = ∫ ( 9t² + 2t + C₁)dt = 9 * t³/3 + 2 * t²/2 + C₁t + C₂ = 3t³ + t² + C₁t + C₂.
При t = 0 ds/dt = 9*0² + 2* 0 + C₁ = 5 ; C₁ = 5 ;
s ( 0 ) =4 = 3* 0³ + 0² + C₁* 0 + C₂ ; C₂ = 4 .
Отже , s( t ) = 3t³ + t² + 5t + 4 - шуканий частинний розв"язок