Найдите 2 числа, значение суммы которых равно: 1) 12, значение разности- 6; 2) 55, значение разности- 25 3) -13, значение разности- 1; 4) 3, значение разности- (-13); 5) 10, значение разности- 5,84; 6) 5/56, значение разности- 1/168 решите с составления систем уравнений заранее

Ответы

gbafujhobr 06.10.2020 05:39

Пошаговое объяснение:

{х + у = 12

{х - у = - 6

метод сложения:

x + y + x - y = 12 + (-6)

2х=6

х=3

3+у = 12

у = 12-9

у = 9

ответ: (3 ; 9)

{х + у = 55

{x - y = -25

x+y+x-y = 55 + (-25)

2x = 30

x= 15

15 + y = 55

y= 55-15

y=40

ответ: (15 ; 40)

{x + y = -13

{x - y = - 1

x+y+x-y = -13 + (-1)

2x = -14

x = -7

-7 + y = -13

y = - 13 + 7

y = -6

ответ: (-7 ; - 6)

{x + y = 3

{x - y = -13

x+y+x-y = 3 + (-13)

2x = -10

x = -10 /2

x = -5

-5 + y = 3

y = 3+5

y = 8

ответ: (- 5 ; 8)

{x + y = 10

{x - y = - 5.84

x + y + x - y = 10 + (-5.84)

2x = 4.16

x = 4.16 : 2

x = 2.08

2.08 + y = 10

y = 10 - 2.08

y = 7.92

ответ : (2,08 ; 7,92 )

{x + y = 5/56

{x - y = - 1/168

x + y + x - y = 5/56 - 1/168

2x = 15/168 - 1/168

2x = 14/168

2x = 1/12

x = 1/12 : 2

х = 1/24

1/24 + у = 5/56

у = 5/56 - 1/24 = 15/168 - 7/168

у = 8/168

у = 1/21

ответ : ( 1/24; 1/21)

ПОКАЗАТЬ ОТВЕТЫ

Hellwood12 06.10.2020 05:39

1) 9 и 3

2) 40 и 15

3) -6 и -7

4) -5 и 8

5) 7,92 и 2,08

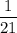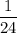
6) $\dfrac{1}{21}$ и $\dfrac{1}{24}$

Пошаговое объяснение:

Во всех задачах первое число обозначим через x, а второе число - через y.

$\displaystyle 1)\; \left \{ {{x+y=12} \atop {x-y=6}} \right. \Leftrightarrow \left \{ {{(6+y)+y=12} \atop {x=6+y}} \right. \Leftrightarrow \left \{ {{2 \cdot y=12-6} \atop {x=6+y}} \right. \Leftrightarrow\\\\\Leftrightarrow \left \{ {{2 \cdot y=6} \atop {x=6+y}} \right. \Leftrightarrow \left \{ {{y=6:2=3} \atop {x=6+3=9}} \right.$

$\displaystyle 2)\; \left \{ {{x+y=55} \atop {x-y=25}} \right. \Leftrightarrow \left \{ {{(25+y)+y=55} \atop {x=25+y}} \right. \Leftrightarrow \left \{ {{2 \cdot y=55-25} \atop {x=25+y}} \right. \Leftrightarrow\\\\\Leftrightarrow \left \{ {{2 \cdot y=30} \atop {x=25+y}} \right. \Leftrightarrow \left \{ {{y=30:2=15} \atop {x=25+15=40}} \right.$

$\displaystyle 3)\; \left \{ {{x+y=-13} \atop {x-y=1}} \right. \Leftrightarrow \left \{ {{(1+y)+y=-13} \atop {x=1+y}} \right. \Leftrightarrow \left \{ {{2 \cdot y=-13-1} \atop {x=1+y}} \right. \Leftrightarrow\\\\\Leftrightarrow \left \{ {{2 \cdot y=-14} \atop {x=1+y}} \right. \Leftrightarrow \left \{ {{y=-14:2=-7} \atop {x=1-7=-6}} \right.$

$\displaystyle 4)\; \left \{ {{x+y=3} \atop {x-y=-13}} \right. \Leftrightarrow \left \{ {{(y-13)+y=3} \atop {x=y-13}} \right. \Leftrightarrow \left \{ {{2 \cdot y=3+13} \atop {x=y-13}} \right. \Leftrightarrow\\\\\Leftrightarrow \left \{ {{2 \cdot y=16} \atop {x=y-13}} \right. \Leftrightarrow \left \{ {{y=16:2=8} \atop {x=8-13=-5}} \right.$

$\displaystyle 5)\; \left \{ {{x+y=10} \atop {x-y=5,84}} \right. \Leftrightarrow \left \{ {{(5,84+y)+y=10} \atop {x=5,84+y}} \right. \Leftrightarrow \left \{ {{2 \cdot y=10-5,84} \atop {x=5,84+y}} \right. \Leftrightarrow\\\\\Leftrightarrow \left \{ {{2 \cdot y=4,16} \atop {x=5,84+y}} \right. \Leftrightarrow \left \{ {{y=4,16:2=2,08} \atop {x=5,84+2,08=7,92}} \right.$

$\displaystyle 6)\; \left \{ {{x+y=\dfrac{5}{56} } \atop {x-y=\dfrac{1}{168} }} \right. \Leftrightarrow \left \{ {{(\dfrac{1}{168}+y)+y=\dfrac{5}{56}} \atop {x=\dfrac{1}{168}+y}} \right. \Leftrightarrow \left \{ {{2 \cdot y=\dfrac{5}{56}-\dfrac{1}{168}} \atop {x=\dfrac{1}{168}+y}} \right. \Leftrightarrow$

$\displaystyle \Leftrightarrow \left \{ {{2 \cdot y=\dfrac{15}{168}-\dfrac{1}{168}} \atop {x=\dfrac{1}{168}+y}} \right. \Leftrightarrow \left \{ {{2 \cdot y=\dfrac{14}{168}} \atop {x=\dfrac{1}{168}+y}} \right. \Leftrightarrow \left \{ {{2 \cdot y=\dfrac{1}{12}} \atop {x=\dfrac{1}{168}+y}} \right. \Leftrightarrow \\\\\Leftrightarrow \left \{ {{y=\dfrac{1}{12}:2=\dfrac{1}{12 \cdot 2}=\dfrac{1}{24}} \atop {x=\dfrac{1}{168}+\dfrac{1}{24}=\dfrac{1}{168}+\dfrac{7}{168}=\dfrac{8}{168}=\dfrac{1}{21}}} \right.$