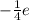Наименьшее значение функции y= (x+8)e(x+9) на отрезке [-10; -8] равно ###
Другие вопросы по теме Математика
Популярные вопросы
- Які повчальні моменти містить твір Чайка Джонатан Лівінгстон ?...
1 - Составить кластер на тему село...
2 - Т. Шевченко з’явився в моєму житті, коли я була маленькою. Читаючи твори...
3 - До ть будь ласка терміново заздалегідь дякую заранее благодарю.) ...
1 - какие биотические факторы влияют на домашних животных?( например на коров...
2 - Напишите все уравнения касательных,выходящих из точки (4,0) к окружности...
1 - (твір Місце для дракона)1. Чому королівство стало занепадати? Хто винен...
1 - Какие виды изомерии характерны для алкенов?Приведите примеры...
1 - В какой стране производят самолёты? 1)Италия 2)Германия 3)Франция 4)Чехия...
1 - Физика физика физика физика ...
1
Пошаговое объяснение:
Найдём производную функции y. y' = ((x+8)(x+9)e)'=((x+8)(x+9))'e=((x+8)'(x+9)+(x+8)(x+9)')e=((1+0)(x+9)+(x+8)(1+0))e=(2x+17)e
Приравняем производную к нулю, чтобы найти точки возможного экстремума. (2x+17)e=0 ⇔ 2x+17=0⇔ x = =-8.5. Найдем знаки производной слева и справа от точки -8.5 на промежутке [-10; -8], слева производная будет отрицательна, слева положительна, а значит функция y будет принимать в точке -8.5 наименьшее значение.
=-8.5. Найдем знаки производной слева и справа от точки -8.5 на промежутке [-10; -8], слева производная будет отрицательна, слева положительна, а значит функция y будет принимать в точке -8.5 наименьшее значение.
Найдем y(-8.5)= (-8.5+8)e(-8.5+9)= -0.5*e*0.5=-0.25e=