Напишите все уравнения касательных,выходящих из точки (4,0) к окружности

Ответы

thiiagooBR 24.08.2020 11:57

(x-1)^2+y^2=4

Рассмотрим полуокружность, расположенную в верхней полуплоскости. Для нее выразим у:

y^2=4-(x-1)^2

$y=\sqrt{4-(x-1)^2}$

Необходимо найти касательную к графику функции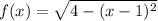 $f(x)=\sqrt{4-(x-1)^2}$ , проходящую через точку $(4;\ 0)$ .

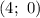Пусть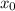 x_0 - точка касания. Уравнение касательной:

y_k=f(x_0)+f'(x_0)(x-x_0)

$f(x_0)=\sqrt{4-(x_0-1)^2}$

Найдем производную:

$f'(x)=\dfrac{1}{2\sqrt{4-(x-1)^2}} \cdot(4-(x-1)^2)'=$

$=\dfrac{1}{2\sqrt{4-(x-1)^2}} \cdot(-2(x-1))=-\dfrac{x-1}{\sqrt{4-(x-1)^2}}$

$f'(x_0)=-\dfrac{x_0-1}{\sqrt{4-(x_0-1)^2}}$

Подставим все величины в уравнение касательной:

$y_k=\sqrt{4-(x_0-1)^2}-\dfrac{x_0-1}{\sqrt{4-(x_0-1)^2}}\cdot(x-x_0)$

Поскольку касательная проходит через точку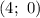 $(4;\ 0)$ , то подставим координаты этой точки в уравнение:

$0=\sqrt{4-(x_0-1)^2}-\dfrac{x_0-1}{\sqrt{4-(x_0-1)^2}}\cdot(4-x_0)$

$\dfrac{(x_0-1)(4-x_0)}{\sqrt{4-(x_0-1)^2}}=\sqrt{4-(x_0-1)^2}$

(x_0-1)(4-x_0)=4-(x_0-1)^2

4x_0-x_0^2-4+x_0=4-x_0^2+2x_0-1

4x_0-4+x_0=4+2x_0-1

3x_0=7

$x_0=\dfrac{7}{3}$

Значит, уравнение касательной имеет вид:

$y_k=\sqrt{4-\left(\dfrac{7}{3} -1\right)^2}-\dfrac{\dfrac{7}{3}-1}{\sqrt{4-\left(\dfrac{7}{3}-1\right)^2}}\left(x-\dfrac{7}{3}\right)$

$y_k=\sqrt{4-\left(\dfrac{4}{3}\right)^2}-\dfrac{\dfrac{4}{3}}{\sqrt{4-\left(\dfrac{4}{3}\right)^2}}\left(x-\dfrac{7}{3}\right)$

$y_k=\sqrt{4-\dfrac{16}{9}}-\dfrac{\dfrac{4}{3}}{\sqrt{4-\dfrac{16}{9}}}\left(x-\dfrac{7}{3}\right)$

$y_k=\sqrt{\dfrac{20}{9}}-\dfrac{\dfrac{4}{3}}{\sqrt{\dfrac{20}{9}}}\left(x-\dfrac{7}{3}\right)$

$y_k=\dfrac{\sqrt{20} }{3}-\dfrac{4\cdot3}{3\sqrt{20} }\left(x-\dfrac{7}{3}\right)$

$y_k=\dfrac{\sqrt{20} }{3}-\dfrac{4}{\sqrt{20} }\left(x-\dfrac{7}{3}\right)$

$y_k=\dfrac{2\sqrt{5} }{3}-\dfrac{4}{2\sqrt{5} }\left(x-\dfrac{7}{3}\right)$

$y_k=\dfrac{2\sqrt{5} }{3}-\dfrac{2}{\sqrt{5} }\left(x-\dfrac{7}{3}\right)$

$y_k=\dfrac{2\sqrt{5} }{3}-\dfrac{2}{\sqrt{5} }x+\dfrac{2}{\sqrt{5} }\cdot\dfrac{7}{ 3}\right)$

$y_k=-\dfrac{2}{\sqrt{5} }x+\dfrac{14}{3\sqrt{5} }+\dfrac{2\sqrt{5} }{3}$

$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{14\sqrt{5}+2\sqrt{5}\cdot5 }{3\cdot5 }$

$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{14\sqrt{5}+10\sqrt{5}}{3\cdot5 }$

$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{24\sqrt{5}}{3\cdot5 }$

$y_k=-\dfrac{2\sqrt{5} }{5 }x+\dfrac{8\sqrt{5}}{5 }$

$y_k=-\dfrac{2\sqrt{5} }{5 }\Big(x-4\Big)$

Полуокружность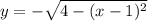 $y=-\sqrt{4-(x-1)^2}$ , расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична: