Наименьшее общее кратное двух чисел равно 120, а наибольший общий делитель составляет 5 % от наименьшего общего кратного.
Найдите эти числа, если разность частных от деления на наибольший
общий делитель равна 1.
Другие вопросы по теме Математика
Популярные вопросы
- Подскажите какое проверочное слово к слову улетели...
3 - Построить ув53 от соль,ля и си бемоль...
2 - На складе было 3 т муки. в первый магазин отгрузили 6 ц муки, а во второй...
3 - Заряд q=1нкл перемещается под действием сил поля из одной точки поля в другую,...
1 - Тело массой 3 кгброшено вертикально вверх скоростью 2 м/с.вычислите максимальную...
3 - Велосипедист проехал 32 километров что составило 4/9 всего пути .сколько...
3 - 1. расставь события в хронологическом порядке а. правление карла великого...
1 - Можно ли получить заряд равный 1,6*10-20кл, 1,6*10-18кл, -1,6*10-20кл? ответ...
3 - Найдите плотность вещества из которого изготовлен кубик если длина его ребра...
1 - Напишите хотябы 5 вещей которые вы можете сделать что бы выбрасывать меньше...
2
Пошаговое объяснение:
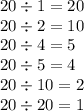
у нас получился ряд частных от деления: 1, 2, 4, 5, 10, 20. Каждое умножим на НОД: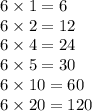
из условия сказано что разность раана 1, то нам подходит разность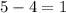
Соответственно числа 24 и 30 являются искомыми.