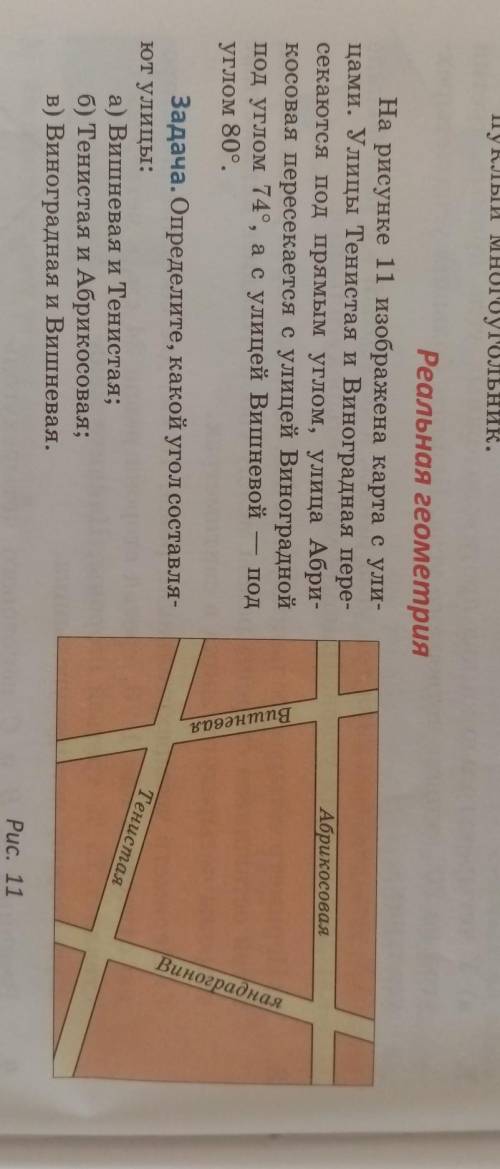
На рисунке 11 изображена карта с ули- цами. Улицы Тенистая и Виноградная пере-
секаются под прямым углом, улица Абри-
косовая пересекается с улицей Виноградной
под углом 74°, ас улицей Вишневой
под
углом 80°.
Вишневая
Задача. Определите, какой угол составля-
ют улицы:
а) Вишневая и Тенистая;
б) Тенистая и Абрикосовая;
в) Виноградная и Вишневая.
Три совета:
Другие вопросы по теме Математика
Популярные вопросы
- Для позакласного читання учневі треба причитати книжку,в якій 152 сторінки.він...
2 - Расставь коэффициенты: k2cr2o7+ki+h2so4=cr2(so4)3+i2+k2so4+ +h2o...
3 - Фонетический разбор слова обрывалось...
3 - Вылезают фонетический разбор слова 2 класс...
1 - Составьте предложение чтобы данные слова что бы были словами категории...
1 - Решить по ! ? в двух пачках 270 тетрадей. сколько тетрадей в каждой...
2 - Подготовьте презентацию составленных словариков и поэтических строк...
3 - Чем жизненные условия в спарте отличались от условий в афинах?...
3 - Лиературный герой, с котрым я хотел бы дружить ( по произведениям раздела...
2 - Почему чехов назвал свой рассказ хамелеон ?...
1
а) Чтобы найти угол между улицами Вишневой и Тенистой, нам нужно вычислить разность между 90° (прямым углом) и углом между улицами Вишневой и Виноградной. На рисунке мы видим, что угол между улицами Вишневой и Виноградной составляет 80°. Таким образом, угол между улицами Вишневой и Тенистой будет равен 90° - 80° = 10°.
б) Угол между улицами Тенистой и Абрикосовой можно найти, используя сумму углов треугольника. Мы знаем, что сумма углов в треугольнике равна 180°. На рисунке видно, что угол между улицами Виноградной и Вишневой составляет 80°, а угол между улицами Виноградной и Абрикосовой равен 74°. Таким образом, угол между улицами Вишневой и Абрикосовой будет равен 180° - (80° + 74°) = 26°.
в) Угол между улицами Виноградной и Вишневой можно также найти методом вычитания углов. Здесь нет прямого угла, поэтому сможем использовать угол между улицами Виноградной и Вишневой, который составляет 80°. Поскольку мы знаем, что сумма углов в треугольнике равна 180°, мы можем вычислить угол между улицами Виноградной и Тенистой следующим образом: 180° - (80° + 90°) = 10°.
Итак, ответы на задачу:
а) Угол между улицами Вишневой и Тенистой равен 10°.
б) Угол между улицами Тенистой и Абрикосовой равен 26°.
в) Угол между улицами Виноградной и Вишневой равен 10°.
Надеюсь, это решение будет понятно для школьника! Если у вас возникнут дополнительные вопросы, пожалуйста, укажите их.