Многочлены Р и Q таковы, что для любого вещественного Х, Р(х^2-х+1) = Q(х^2+x+1). Докажите, что Р и Q - константы.

Ответы

arutik5 23.10.2020 01:28

Пусть не так, и Р и Q - многочлены степени не ниже 1.

$P(x^2-x+1) = Q(x^2+x+1)\\ x\to x-1=x^2-x+1\to (x-1)^2-(x-1)+1=x^2-2x+1-x+1+1=x^2-3x+3, \;x^2+x+1\to(x-1)^2+x-1+1=x^2-x+1=\\ =P(x^2-3x+3) = Q(x^2-x+1)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1)\\ x\to -x=x^2-x+1\to (-x)^2-(-x)+1=x^2+x+1, \;x^2+x+1\to(-1)^2+(-x)+1=x^2-x+1=\\ =P(x^2+x+1) = Q(x^2-x+1)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(2)\\ (1),(2)=P(x^2+x+1) = P(x^2-3x+3)$

$x^2+x+1=(x+\dfrac{1}{2})^2+\dfrac{3}{4}$ - парабола с вершиной в точке $(-\dfrac{1}{2};\dfrac{3}{4})$ , ветви направлены вверх.

$x^2-3x+3=(x-\dfrac{3}{2})^2+\dfrac{3}{4}$ - парабола с вершиной в точке $(\dfrac{3}{2};\dfrac{3}{4})$ , ветви направлены вверх.

$x=2=P(7) = P(1)\\ x^2-3x+3=7=x^2-3x-4=0=x=4\\ x=4=P(21)=P(7)\\ x^2-3x+3=21=x^2-3x-18=0=x=6\\ x=6=P(43)=P(21)$

Пусть подобными действиями было получено значение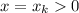 x=x_k0

$x=x_k=P(x_k^2-3x_k+3) = P(x_k^2+x_k+1)\\ x^2-3x+3=x_k^2+x_k+1=x^2-3x+(-x_k^2-x_k+2)=0=x=\dfrac{3\pm\sqrt{4x_k^2+4x_k+1}}{2}=\dfrac{3\pm(2x_k+1)}{2}$

Выберем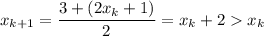 $x_{k+1}=\dfrac{3+(2x_k+1)}{2}=x_k+2x_k$ . Получим, что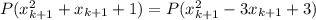 $P(x_{k+1}^2+x_{k+1}+1)=P(x_{k+1}^2-3x_{k+1}+3)$

$x_{k+1}^2-3x_{k+1}+3=(x_k+2)^2-3(x_{k}+2)+3=x_k^2+4x_k+4-3x_k-6+3=x_k^2+x_k+1=P(x_{k+1}^2-3x_{k+1}+3) = P(x_k^2+x_k+1)=\\ =P(x_{k+1}^2+x_{k+1}+1)=P(x_k^2+x_k+1)$

Т.е. построена монотонно возрастающая последовательность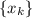 $\{x_k\}$ такая, что 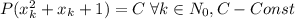$P(x_k^2+x_k+1)=C\;\forall k\in N_0, C-Const$ . Очевидно, т.к. последовательность не ограничена сверху, то в ней бесконечное число членов => многочлен 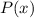P(x) принимает значение 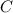в бесконечном числе точек => тогда он будет иметь вид $P(x)=Q(x)(\prod\limits_{k=0}^\infty (x-(x_k^2+x_k+1))+C)$ , а значит его степень бесконечна, что невозможно.

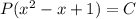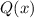А тогда P(x)=C , откуда P(x^2-x+1) = C , следовательно Q(x^2+x+1)=C . Т.е. на множестве $\{x|x=t^2+t+1,t\in R\}=[\dfrac{3}{4};+\infty)$ с бесконечным числом элементов многочлен Q(x) принимает значение 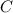. А тогда, по аналогии с предыдущим пунктом, Q(x)=C