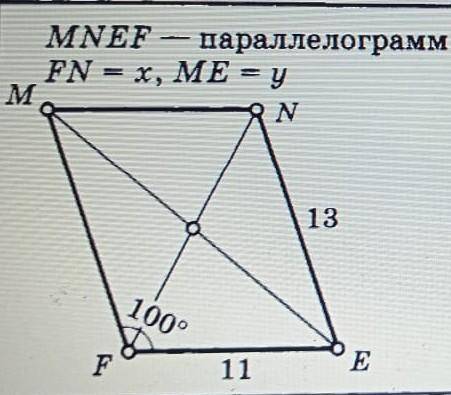
Mnef параллелограмм fn=x me=y, fe=11, ne=13​

По синусас можно определить, что 11+13=24

Давайте разберемся с данным вопросом.

По условию дан параллелограмм MNEF, где FM = x, ME = y, FE = 11 и NE = 13.

Первым шагом, вспомним некоторые основные свойства параллелограмма. В параллелограмме противолежащие стороны равны и противоположные углы равны.

Так как даны длины сторон, мы можем использовать эти свойства для решения задачи.

Рассмотрим стороны параллелограмма:
MN = EF (противолежащие стороны параллелограмма равны)
FM = x
ME = y

Также у нас есть информация, что FE = 11 и NE = 13.

Мы можем использовать эти данные для составления уравнений.

Уравнение 1: NM = EF (противолежащие стороны параллелограмма равны)
Уравнение 2: FM + ME = EF (сумма противолежащих сторон равна третьей стороне треугольника)

Подставив известные значения, получим:

Уравнение 1: NM = EF => NM = 11
Уравнение 2: x + y = 11

Для решения уравнения необходимо уточнить значения x и y.

Мы также знаем, что противоположные углы параллелограмма равны. В этом случае, мы можем использовать соответствующие углы для нахождения значений x и y.

Возьмем треугольник MEF и рассмотрим угол M и угол E.

По свойству параллелограмма, эти углы равны.

Угол M равен углу E, поэтому можно записать уравнение:

Угол M = угол E
Угол M = угол E = 180 - угол F

Теперь мы можем использовать теорему косинусов для выражения угла M через стороны FM, ME и EF:

cos(M) = (FM^2 + ME^2 - EF^2) / (2 * FM * ME)

Подставим известные значения:

cos(M) = (x^2 + y^2 - 11^2) / (2 * x * y)

Так как угол M и угол E равны, мы можем использовать теорему косинусов для выражения угла E через стороны FM, ME и EF:

cos(E) = (FM^2 + ME^2 - EF^2) / (2 * FM * ME)

Подставим значения сторон и угла F (90 градусов):

cos(E) = (x^2 + y^2 - 11^2) / (2 * x * y)

Так как угол M и угол E равны, мы можем записать:

cos(M) = cos(E)

(x^2 + y^2 - 11^2) / (2 * x * y) = (x^2 + y^2 - 11^2) / (2 * x * y)

Теперь мы можем решить это уравнение.

Перенесем все в одну часть:

(x^2 + y^2 - 11^2) / (2 * x * y) - (x^2 + y^2 - 11^2) / (2 * x * y) = 0

Упростим выражение:

0 = 0

Таким образом, у нас нет решения для этого уравнения. Мы не можем найти конкретные значения для x и y, учитывая данные в условии задачи.

В итоге, ответ на вопрос "Mnef параллелограмм fn=x me=y, fe=11, ne=13?" - описанный параллелограмм не удовлетворяет условиям задачи, так как не существуют конкретные значения для x и y, учитывая заданные длины сторон FE и NE.