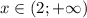Log₇ (4x – 6) > log₇ (2x – 4)
Другие вопросы по теме Математика
Популярные вопросы
- Решить эти примеры а) 13056: 32*704+(4301-39*+12622): 300 б) (15062-917): 69-520*750:...
3 - Укажите количество грамматических основ в предложении 18. ответ запишите цифрой....
1 - Вычислите объем углекислого газа, который образуется при сгорании 6 кг угля (формула...
3 - Как правильно пишется заоблачный или заоблочный?...
1 - Что означает выражение стыдливый из за стола голодный встаёт...
2 - Можно ли с отрицательно заряженной палочки зарядить тело положительным зарядом?...
2 - Склади і запиши невеликий твір на тему що було б,якби всі українці були як одна...
1 - Отгадать загадку париж что находится посреди него...
1 - Сколько целыx чисел расположено между числами -157 и 44...
2 - Белок содержит 5% аргинина. чему равна минимальная относительная масса этого белка,...
1
Пошаговое объяснение:
ОДЗ:
4x-6>0 x>1,5
2x-4>0 x>2
4x-6>2x-4
2x>2
x>1
пересекаем с ОДЗ и получаем ответ x∈(2;+∞)
Данное неравенство равносильно системе:
Общим решением будет интервал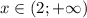
ответ: