Какова наибольшая возможная площадь у треугольника со сторонами a,b,c если известно, что ?
Другие вопросы по теме Математика
Популярные вопросы
- 6)под влиянием каких условий формируется характер? а)наследственность,общественной...
2 - 3\5 его равны 90 найдите число,если-...
3 - Расстояние между городом и зимовкой 150 км. из города к зимовке выехали аэросани...
3 - Купили 3 пакетика семян гороха по 2р.и столько же пакетиков свеклы по 4р.сколькл...
3 - Скласти розповидь на тему зимова екскурсия 2 клас....
2 - Где на планете зафиксированы максимальная и минимальная температуры воздуха?...
1 - Впрямоугольном треугольнике abc с гипотенузой bc,провели высоту ad,угол b равен...
2 - Ядро имеется- (выберите все верные ответы) 1.в зрелых члениках ситовидных трубок...
3 - Решить для настольного станка используется дпт с параллельным возбуждением...
2 - Определите какой картой пользовались герои романа марка твена !...
2
Пусть угол между сторонами a и b равен φ. Тогда площадь треугольника равна ; Пусть произведение ab максимально, то есть равно 6. Сторона c не участвует в формировании величины площади. Однако от c зависит максимальность синуса. По теореме косинусов:
; Пусть произведение ab максимально, то есть равно 6. Сторона c не участвует в формировании величины площади. Однако от c зависит максимальность синуса. По теореме косинусов: 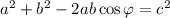 ; Подставив максимальные значения a и b, а также минимальное значение косинуса ⇔ максимальное значение синуса, придем к тому, что
; Подставив максимальные значения a и b, а также минимальное значение косинуса ⇔ максимальное значение синуса, придем к тому, что  , при этом значение c лежит в диапазоне. Итак, максимальная площадь треугольника равна
, при этом значение c лежит в диапазоне. Итак, максимальная площадь треугольника равна 