Как это вычеслить интеграл
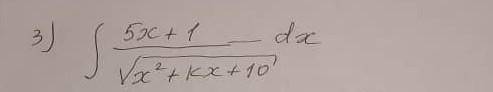
Другие вопросы по теме Математика
Популярные вопросы
- Участок квадратной формы 30метров на 30 м засадили морковью.сколько грамм...
3 - Бидон на 2/5-ю часть наполнен водой. если в бидон влить 14 л воды, то он...
3 - Написать эссе на тему роль медицины в нашей жизни на языке...
3 - 1. дан прямоугольник со сторонами 5 дм и 35 см. меньшую сторону увеличили...
1 - Сравните в диаграмме венна гюлистанский и туркменчайский договора...
1 - Угол при вершине противолежащей основанию равнобедренного треугольника равен...
1 - Надо написать: твір мініатюра чи погоджуюсь я з тим, що люди які читають...
2 - Если y равен 7 тогда 0,48 y - 0,2 y + 0,52 y=...
2 - Пропуск у реченні можна запомнити кожним із зазначених прийменників окрім...
3 - Найти область определения функции: 1) y=6/x^2-16 2) y=5+6x/2x-4...
1
В числителе делаем производную знаменателя:
(x^2+kx+10)' = 2x+k
В первом интеграле числитель вносим под знак дифференциала
Во втором интеграле в знаменателе выделяем квадрат суммы:
Получаем:
Получаем: