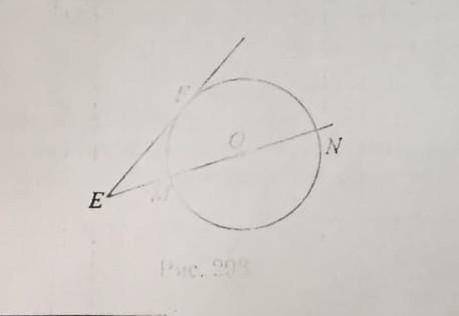
К окружности с центром в точке О проведены касательная EF ( F - точка касания) и секущая ЕО, пересекающая окружность в точках М и N. Найдите MN, если EF=24, EO=25
Другие вопросы по теме Математика
Популярные вопросы
- Ав какой ревизии nintendo switch отклеивался ...
1 - 100 при каких значениях параметра a хотя бы один корень уравнения...
2 - Вертолет массой 2000 кг поднимает груз массой 1000 с постоянной скоростью...
1 - Напишити по произведение ,, вопросы: 1 кто главные герои рассказа?...
3 - 1. найдите в тексте неполное предложение. выпишите, расставляя знаки...
1 - Составьте сложноподчинённые изъяснительные предложения используя в...
3 - Прочитайте отрывки из писем а п чехова и высказывания о нем современников...
3 - H2o2 и br2. выяснить, у кого окислительная больше, опираясь на справочные...
2 - Много рисунок части кожицы листа .расскажите о строении устьица.напишите...
1 - 2. найдите промежутки возрастания f(x) = tg(x- п/4) на отрезке [0;...
1
По теореме о касательной и секущей проведенной из точки к окружности :
(здесь можно и без этой, т.к. секущая проходит через центр окр и ΔEMO известно).
EF² = EM *EN , где M и N точки пересечения секущей с окружностью
( EM_секущая , а EN внешняя часть секущей ) .
EF² =(EO +OM)(EO - ON) ;
EF² =(EO +R)(EO - R) ;
EF² =EO² - R² ;
R = √(EF² - EO²) ;
R = √(25² - 7²) = √(25 -7)(25 +7) =√18*32 =√9*2*2*16 =2*3*4 =24
Пошаговое объяснение: