1. Математика
  2. Если cosx=1/10, то вычислите

Если cosx=1/10, то вычислите (1+tg^x)(1-sin^2x)-sin^2x

можно подробнее

Юшут Юшут    3   25.07.2019 22:59    2

Ответы
Makc920 Makc920  13.08.2020 22:22

Первое слагаемое в первой скобке воспользуемся известным тождеством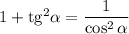 1+{\rm tg}^2\alpha=\dfrac{1}{\cos^2\alpha}, а во второй скобке применим основное тригонометрическое тождество

\displaystyle \left(1+{\rm tg}^2x\right)\left(1-\sin^2 x\right)-\sin^2x=\dfrac{1}{\cos^2x}\cdot \cos^2x-\sin^2x=1-\sin^2x=\cos^2x

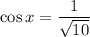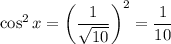
Если \cos x=\dfrac{1}{\sqrt{10}}, то \cos^2x=\left(\dfrac{1}{\sqrt{10}}\right)^2=\dfrac{1}{10}

ПОКАЗАТЬ ОТВЕТЫ
lili2018 lili2018  13.08.2020 22:22

A) 0.1

Пошаговое объяснение:

(1 + {\tan(x)}^{2} )( 1 - { \sin(x) }^{2} ) - {\sin(x)}^{2} = (1 + {( \frac{ \sin(x) }{ \cos(x) } })^{2} ) \times {\cos(x)}^{2} - {\sin(x)}^{2} = \frac{ { \cos(x) }^{2} + { \sin(x) }^{2} }{ { \cos(x) }^{2} } \times { \cos(x) }^{2} - { \sin(x) }^{2} = { \cos(x) }^{2} + { \sin(x) }^{2} - { \sin(x) }^{2} = { \cos(x) }^{2}

При

\cos(x)=\frac{1}{\sqrt{10}}

Получим:

{ \cos(x)}^{2} = {( \frac{1}{ \sqrt{10} } )}^{2} = 0.1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
lerakuznyak lerakuznyak  23.05.2019 18:20
1)4y-11=y+2,5 2)1,5+1,2+2y+0,8=2,7 решите уровнения с пояснением...
Варя0601 Варя0601  23.05.2019 18:20
Дан треугольник abc со сторонами ab=7, bc=8, ac=9 на отрезке какой длины делит биссектриса bd сторону ac...
vaider222 vaider222  23.05.2019 18:20
1) запишіть яке-небудь натуральне число , яке більше за 2364 і менше від 2432, що містить цифру 8 у розряді одиниць. скільки таких чисел можна записати ? запишіть найменше...
Покемон123456789 Покемон123456789  23.05.2019 18:20
Розгорнутий кут поділили внютрішним променями на рівні кути знайдіть градусну міру цих кутів, якщо отримано: 1) 2 кути 2) 4 кути 3) 6 кутів іть дуже требе...
Andy01 Andy01  23.05.2019 18:20
Какого данного не хватает,чтобы решить ? . один ученик купил тетрадь и ручку за 37 руб., а другой купил тетрадь и ручки за 49 руб. сколько стоили тетрадь и ручка отдельно?...
kirillyamont2 kirillyamont2  23.05.2019 18:10
Два угла треугольника равны 34° и 112°. какова величина третьего угла этого треугольника? к какому виду относится этот треугольник? этот и...
RGROP17 RGROP17  23.05.2019 18:10
Три участника команды по стрельбе показали такие результаты.антон выбил 22 очка,боря -28,а витя на три очка меньше бори.придумай вопросы.найди ответы...
Domashkafu Domashkafu  23.05.2019 18:10
«сколько учеников в вашем классе? », - спросил яша у гали. галя, подумав сказала: «если отнять от наибольшего двузначного числа число, записанное двумя восьмёрками,...
RuslanVil RuslanVil  23.05.2019 18:10
Найти наибольшее произведение x*y, когда 3x+4y=12...
pallnash pallnash  23.05.2019 18:10
Запишите все натуральные числа которые больше 495 и меньше 502...

Популярные вопросы