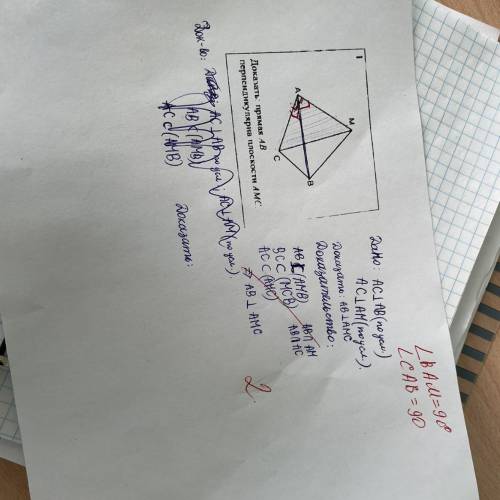
Доказать: прямая AB перпендикулярна плоскости AMC. дано: угол BAM=90, угол CAB=90

Для доказательства того, что прямая AB перпендикулярна плоскости AMC, мы можем использовать свойство ортогональности векторов.

1. Рассмотрим векторы AB и AM.
Возьмем точку A в качестве начала координат и рассмотрим векторы AB и AM.
Вектор AB представляет собой разность координат точек B и A, то есть AB = B - A.
Аналогично, вектор AM представляет собой разность координат точек M и A, то есть AM = M - A.

2. Покажем, что векторы AB и AM ортогональны.
Для этого нам потребуется воспользоваться свойством ортогональности векторов, которое гласит: два вектора ортогональны, если и только если их скалярное произведение равно нулю.

3. Рассмотрим скалярное произведение векторов AB и AM.
AB • AM = (B - A) • (M - A)

(где • обозначает скалярное произведение векторов)

4. Раскроем скалярное произведение векторов.
AB • AM = (Bx - Ax)(Mx - Ax) + (By - Ay)(My - Ay) + (Bz - Az)(Mz - Az)

(где Bx, By, Bz - координаты точки B, Mx, My, Mz - координаты точки M, Ax, Ay, Az - координаты точки A)

5. Разложим выражение для краткости.
AB • AM = (Bx - Ax)(Mx - Ax) + (By - Ay)(My - Ay) + (Bz - Az)(Mz - Az)
= (Bx - Ax)(Mx) - (Bx - Ax)(Ax) + (By - Ay)(My) - (By - Ay)(Ay) + (Bz - Az)(Mz) - (Bz - Az)(Az)

6. Раскроем скобки и упростим выражение.
AB • AM = BxMx - AxMx - BxAx + Ax^2 + ByMy - AyMy - ByAy + Ay^2 + BzMz - AzMz - BzAz + Az^2
= BxMx - AxMx - BxAx + Ax^2 + ByMy - AyMy - ByAy + Ay^2 + BzMz - AzMz - BzAz + Az^2

7. Обратим внимание, что Ax^2 + Ay^2 + Az^2 является квадратом модуля вектора AM.
Аналогично, BxMx + ByMy + BzMz является скалярным произведением вектора B и вектора M.
С учетом этого, мы можем переписать выражение следующим образом:
AB • AM = - (B • A) + AM^2

8. Теперь нам нужно доказать, что AB • AM равно нулю.
У нас есть два условия: BM = 90 и CA = 90. По свойству ортогональности векторов, если скалярное произведение равно нулю, то векторы являются ортогональными.
Таким образом, условия здесь означают, что векторы AB и AM ортогональны.

Итак, мы доказали, что AB • AM = 0, что означает, что векторы AB и AM ортогональны.
Следовательно, прямая AB перпендикулярна плоскости AMC.