Доказать, что при всех натуральных значениях n значение выражения кратное 9

Проще всего доказать это с сравнений. Хотя можно и с метода математической индукции. Говорят, что целые числа a и b сравнимы по модулю k, если a-b делится на k, то есть a=b+kt, t - целое. Пишут так: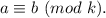 Есть теорема, которая утверждает, что сравнения можно складывать, вычитать, перемножать, возводить в натуральную степень. Имеем:

Это доказывает требуемое утверждение

Представляем:   13^n=(9+4)^n -выражение представляет собой бином Ньютона, в котором каждый член кроме 4^n помножен на какую либо степень  числа 9, таким  образом остаток от  деления  14*13^n на  9  равен остатку от деления  14*4^n  на 9 , то есть: 14*13^n=9*a +14*4^n (а-целое число или  по другому 9*a=14*(cумма  остальных членов бинома) )Тогда: 14*13^n+13*2^2n= 9*a+14*4^n+13*4^n=9a +27*4^n=9*(a+3*4^n)-то есть кратно 9.