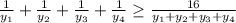Доказать что для произвольных чисел a b c d оправдается равенство 1/а + 1/b + 1/c + 1/c >= 64/(a+b+c+d)

Ответы

andreiantipov1 17.08.2020 18:58

Для начала докажем то, что называется неравенством Коши-Буняковского-Шварца:

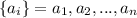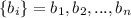Рассмотрим два набора чисел: $\{a_{i}\}=a_{1},a_{2},...,a_{n}$ и $\{b_{i}\}=b_{1},b_{2},...,b_{n}$ .

Тогда выполнено неравенство: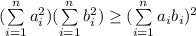 $(\sum\limits_{i=1}^{n}a_{i}^{2})(\sum\limits_{i=1}^{n}b_{i}^{2})\geq (\sum\limits_{i=1}^{n}a_{i}b_{i})^{2}$ ;

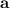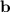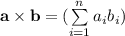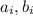Это неравенство можно доказывать по-разному. Заметим, что скалярное произведение векторов $\textbf{a}$ и $\textbf{b}$ есть $\textbf{a}\times\textbf{b}=(\sum\limits_{i=1}^{n}a_{i}b_{i})$ , где $a_{i},b_{i}$ - координаты составляющих вектора. Поскольку скалярное произведение векторов всегда не превосходит произведения модулей векторов (так как 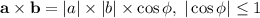$\textbf{a}\times\textbf{b}=|a|\times|b|\times\cos\phi,\; |\cos\phi|\leq 1$ ), то отсюда немедленно следует неравенство (ведь сумма квадратов в рассматриваемом неравенстве - это квадрат модуля вектора).

__________________________

Сделаем замену: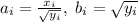 $a_{i}=\frac{x_{i}}{\sqrt{y_{i}}},\; b_{i}=\sqrt{y_{i}}$ ; Получим неравенство: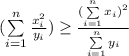 $(\sum\limits_{i=1}^{n}\frac{x_{i}^{2}}{y_{i}} )\geq \frac{(\sum\limits_{i=1}^{n}x_{i})^2}{\sum\limits_{i=1}^{n}y_{i}}$

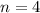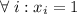Полагая n=4 и $\forall\; i:x_{i}=1$ , получим: $\frac{1}{y_{1}}+\frac{1}{y_{2}}+\frac{1}{y_{3}}+\frac{1}{y_{4}}\geq \frac{16}{y_{1}+y_{2}+y_{3}+y_{4}}$