Доказать 1/(3n+1)+1/(3n+2)+1/3n+3>1/(2n+1)+1/(2n+2) n - натуральное
Другие вопросы по теме Математика
Популярные вопросы
- Визначте основні етапи агресії Російської Федерації проти України....
3 - ПОДСКАЖИТЕ ОЧЕНЬ НУЖНА Доведiть, що твiр Гр. Тютюнника Дивак э оповiданням...
2 - Здравствуйте, тест по химии сделать!...
1 - Ребусты шеш. Сонан соң ана сөзіне екі сөйлем құра. Ол сөз бірінде - бастауыш,...
3 - -3|х|+|5+у| если х= 4,у= -3...
2 - Сумма смежных углов треугольника равна...Сумма углов треугольника равна......
3 - Какое из тел обладают потенциальной энергией? А. Летящий самолет. Б. Сжатая...
1 - Объясните почему связаны слова мудрость помнить мученик. ДКП...
3 - Награды александр германович генкель ...
3 - Передайте следующие предложе¬ния в косвенной речи. 1. Lena said, I saw him...
2
Сильные духом и имеющие некоторый запас времени могут показать, что
Очевидно, эта разность положительна.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Докажем и другим Заметим, что для любого положительного x и для любого положительного 0 < a < x верно следующее:
(Это можно проверить путем домножения на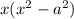 , получится
, получится 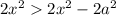 )
)
Тогда
Разность, написанная выше, строго больше, чем
Так как функция y = 1/x убывает для x > 0, то последнее выражение строго положительно.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
По неравенству о средних
откуда
Тогда
После раскрытия скобок в числителе получится n/12, и вся разность по-прежнему положительна.