Для данной функции у и аргумента х0 вычислить у''' (х0)
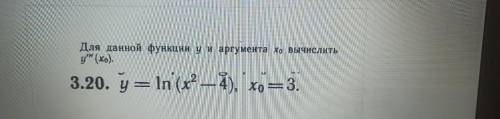
Другие вопросы по теме Математика
Популярные вопросы
- Человек заходит с улицы в неосвещенноепомещение. При этом диаметр...
2 - Найдите точку в которой касательная к графику функции f(x)=корень...
1 - Запятые при причастном обороте Проанализируйте текст и выполните...
3 - Якими членами речення бувають числівники...
3 - Определи вид предложения по цели высказывания и интонации. Алмазы...
2 - Сделать супер-пупер краткий конспект по теме Безопасность в интернете...
3 - Мій улюблений єпизод із повісті баха чайка....
3 - Ціуаві факти про кислотні ...
3 - Какая точка принадлежит графику функции y=2x^+4...
1 - Парни кто свободный? Пишите мне в инстаграм (_v_i_k_a__t_o_p_)...
2
Пошаговое объяснение: