Даны различные натуральные числа x и y такие, что если к x прибавить наибольший де- литель y, отличный от y, то получится тот же результат, что и если к y прибавить наибольший делитель x, отличный от x. Докажите, что один из этих наибольших делителей делится на другой.
Другие вопросы по теме Математика
Популярные вопросы
- Уақыт-өмір тақырыбында эссе жаз....
3 - 1. В чем, по мнению Брена Батаклана, заключается предназначение...
2 - Просклоняйте слова жаттығу, әпке, дәрігерАтау с.Ілік с.Барыс с.Табыс...
1 - Жапалақ жапалақ қар жауса да жазға қалмас мағынасы...
1 - Существует народная примета, что если месяц лежит на боку , то...
3 - 87612.3150 345.381464.4325 318.210626:314628.458248.4110526:3...
3 - До ть розв язати задачу Батько має III групу крові, а дитина IV. Якою...
2 - Выпишите в таблицу детали поведения Дуни в различные моменты ее...
1 - SpeakingComplete the conversation with the words in the box клас...
2 - За круглым столом сидят 8 гномов, у каждого из которых есть по...
1
Пусть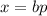 , где
, где 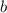 — наибольший собственный делитель
— наибольший собственный делитель  . Аналогично,
. Аналогично, 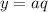 . Без ограничения общности пусть
. Без ограничения общности пусть 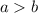 . По условию:
. По условию: 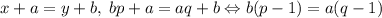 . Пусть
. Пусть 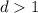 есть общий делитель
есть общий делитель 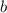 и
и  . Заметим, что
. Заметим, что 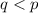 , в самом деле, пусть не так:
, в самом деле, пусть не так: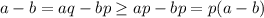 , противоречие. Итак,
, противоречие. Итак, 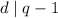 и потому
и потому 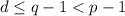 . Так мы нашли делитель
. Так мы нашли делитель 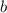 , меньший
, меньший 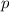 . Значит, если он не равен 1, то
. Значит, если он не равен 1, то 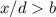 , противоречие. Значит,
, противоречие. Значит, 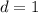 . Следовательно,
. Следовательно, 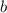 и
и  взаимно просты, откуда
взаимно просты, откуда 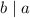 .
.