Дано 25 чисел, причём известно, что сумма любых четырёх из них положительна.объясните, почему положительной будет сумма всех 25 чисел.

Ответы

йцуячс2 01.10.2020 17:07

Порассуждаем не торопясь. Пусть всего чисел не 25, а 5: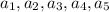 a_1, a_2, a_3, a_4, a_5 . Выпишем все четверки:

a_1, a_2, a_3, a_4;

a_1, a_2, a_3, a_5;

a_1, a_2, a_4, a_5;

a_1, a_3, a_4, a_5;

a_2, a_3, a_4, a_5.

По условию все они положительны. Сложим все эти четверки. Снова получится положительное число. Поскольку каждое из чисел входит ровно в четыре четверки (для дальнейшего важно, что каждое число входит в одинаковое количество четверок), то общая сумма будет иметь вид

4(a_1+a_2+a_3+a_4+a_5)0.

Отсюда и следует утверждение.

Для 25 чисел рассуждение ничем не отличается, только четверок намного больше (те, кто знаком с комбинаторикой, может подтвердить, что всего четверок будет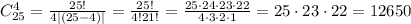 $C_{25}^4=\frac{25!}{4|(25-4)|}=\frac{25!}{4!21!}=\frac{25\cdot 24\cdot 23\cdot 22}{4\cdot 3\cdot 2\cdot 1}=25\cdot 23\cdot 22=12650$ , хотя это абсолютно неважно для решения задачи). Важно только, что каждое из чисел будет входить в одинаковое количество четверок. Неважно, чему равно это количество, но доказывая тезис о том, что все математики страшные зануды, найдем его. Подбирая для конкретного числа "трех соседей", мы тем самым из 24 чисел выбираем три числа, а сделать это можно

$C_{24}^3=\frac{24!}{3!21!}=\frac{24\cdot 23\cdot 22}{3\cdot 2\cdot 1}=4\cdot 23\cdot 22=2024$ Сложив все четверки, а они по условию положительные) мы получим положительное число