Дана окружность с центром в точке а. а(3; 4) b(3; 7) f(0; 4) d(3; 1) e(6; 4) m(6; 7) r^2=9

найти fd диаметр-? , bd диаметр-?

какие точки лежат на окружности а какие нет?

расстояние от начала координат до центра окружности?

Ответы

Юрашевич101 10.10.2020 15:14

ответы в объяснении

Пошаговое объяснение:

Вспомним нужные сведения:

1) Уравнение окружности с центром в точке О(x0; y0) и радиусом r имеет вид: (x-x0)²+(y-y0)²=r².

2) Расстояние от точки T(x1; y1) до точки P(x2; y2) определяется по формуле: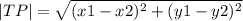 $|TP|=\sqrt{(x1-x2)^{2} +(y1-y2)^{2} }$ .

Решение задачи.

Найдем расстояние |FD| и |BD| :

$|FD|=\sqrt{(0-3)^{2} +(4-1)^{2} }=\sqrt{9+9}=3\sqrt{2}$

$|BD|=\sqrt{(3-3)^{2} +(7-1)^{2} }=\sqrt{0+36} = 6$

Дана окружность с центром в точке А(3; 4) и радиусом r²=9. Тогда уравнение окружности имеет вид:

(x-3)²+(y-4)²=9

Теперь определим, какие точки лежат на окружности а какие нет. Если точка лежит на окружности, то её координаты удовлетворяют уравнение окружности.

А(3;4) : (3-3)²+(4-4)²=0 ≠ 9 , не лежит на окружности!

B(3;7) : (3-3)²+(7-4)²=9 = 9 , лежит на окружности!

F(0;4) : (0-3)²+(4-4)²=9 = 9 , лежит на окружности!

D(3;1) : (3-3)²+(1-4)²=9 = 9 , лежит на окружности!

E(6;4) : (6-3)²+(4-4)²=9 = 9 , лежит на окружности!

M(6;7) : (6-3)²+(7-4)²=18 ≠ 9 , не лежит на окружности!

Теперь определим расстояние от начала координат до центра окружности. Координаты начала координат О(0; 0), а координаты центра окружности А(3; 4):

$|OA|=\sqrt{(0-3)^{2} +(0-4)^{2} }=\sqrt{9+16}=\sqrt{25} =5$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

dragon64 13.12.2021 23:36

слядя 13.12.2021 23:36

mlphappyme 13.12.2021 23:37

trunczova84 13.12.2021 23:37

расставить порядок действий...

pomxic 13.12.2021 23:40

ale2005171112 13.12.2021 23:40

vityastah 10.05.2021 15:53

nastiksergi7 10.05.2021 15:52

можете фоткой умаляю это ...

RoyaIHeII 10.05.2021 15:52

Асыл111111111 10.05.2021 15:51