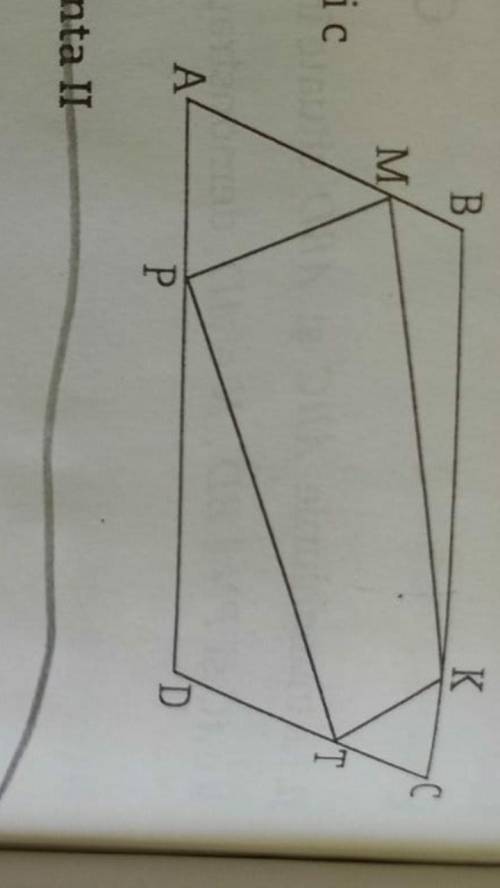
ABCD паралеллограм, AM/CT = AP/CK, но не равно 1. Продемонстрируйте, что MKTP трапеция !

Давайте разберем эту задачу шаг за шагом.

У нас дан параллелограмм ABCD. Нам нужно доказать, что четырехугольник MKTP является трапецией.

Для начала, обратим внимание на заданные отношения.
У нас есть два равенства: AM/CT = AP/CK и они оба не равны 1. Заметим, что AM и CT обе являются диагоналями параллелограмма ABCD, а AP и CK являются его сторонами.

Теперь рассмотрим треугольники AMK и CKT.

По условию задачи, у нас есть, что AM/CT = AP/CK. Заметим, что AM и CT - диагонали параллелограмма и CK и AP - стороны. Это нам подсказывает, что мы можем использовать подобие треугольников для доказательства.

То есть, треугольники AMK и CKT подобны друг другу. Почему это так?

Поскольку мы имеем равенство диагоналей к сторонам (AM/CT = AP/CK), углы треугольников должны быть равными, поскольку они находятся противоположно диагоналям в параллелограмме и подиагональными частями.

Таким образом, угол AMK равен углу CKT. Углы AMK и CKT являются противостоящими углами при основании, поэтому они должны быть равными. Также, у нас есть сторонные стороны AM и CK, которые являются общими для обоих треугольников. Поэтому, по признаку подобия треугольников, треугольники AMK и CKT являются подобными.

Значит, соответствующие углы треугольников MKP и TPK также будут равны. Поскольку угол КТК является внутренним углом параллелограмма АВСD, то угол МАК является прямым углом.

Теперь сравним угол КМК и ТМК. Поскольку уголы КТК и МАК, а также уголы TPK и MKP являются равными, то углы КМК и ТМК будут равными. Таким образом, у нас есть противоположные углы боковых сторон МК и ТК, которые равны, что делает параллелограмм AMKT.

По определению, в параллелограмме противоположные стороны параллельны, поэтому ТК || МК.

Из этого следует, что четырехугольник MKTP является трапецией, поскольку он имеет две параллельные стороны (ТК || МК).

Таким образом, доказано, что MKTP - трапеция.

Надеюсь, это решение понятно. Если у вас есть еще вопросы, не стесняйтесь задавать.

БбБоОО зЗнААаИи ТТтеЕлЛлЕЕрРРаа - @united brai nly (бББеЗзз пПррОббЕЕЕлллооОВВ)