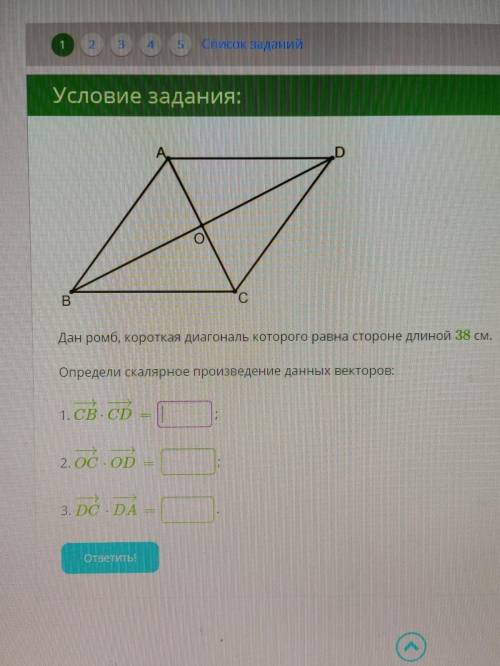
Дан ромб, короткая диагональ которого равна 38 см. определить скалярное произведение данных векторов

Чтобы решить эту задачу, нам необходимо понять, что такое скалярное произведение векторов.

Скалярное произведение двух векторов определяется как произведение длин векторов на косинус угла между ними. Математически, скалярное произведение двух векторов a и b обозначается как a·b.

В данном случае у нас есть два вектора - AC и DB, которые являются диагоналями ромба. Для начала, определим длины этих векторов.

У нас есть одна короткая диагональ равная 38 см. Зная это, мы можем найти длину длинной диагонали, используя свойство ромба, что диагонали взаимно перпендикулярны и делят друг друга пополам.

Поэтому длина длинной диагонали будет также равна 38 см. Теперь, как мы знаем длины векторов, нам нужно найти угол между ними.

Учитывая, что ромб является параллелограммом, углы приложения сил двух диагоналей равны. Это означает, что угол между векторами AC и DB является прямым углом (90 градусов).

Теперь мы можем рассчитать скалярное произведение векторов AC и DB.

Так как угол между векторами является прямым углом, косинус угла будет равен 0. Поэтому скалярное произведение будет равно произведению длин векторов на косинус угла:

AC·DB = |AC| * |DB| * cos(угол между ними)

В нашем случае, длина вектора AC (короткой диагонали) равна 38 см, длина вектора DB (длинной диагонали) также равна 38 см, а cos(90°) = 0.

Подставляя значения в формулу, мы получаем:

AC·DB = 38 см * 38 см * 0

AC·DB = 0

Таким образом, скалярное произведение данных векторов равно нулю.