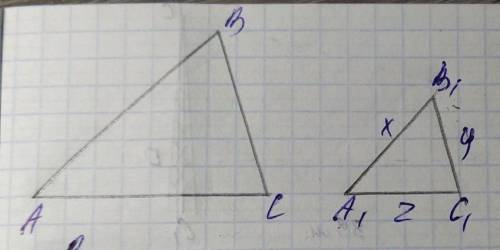
∆АВС относится к ∆А1В1С1
АВ:ВС:АС=9:7:8
x+z=51​

Добрый день! Конечно, я могу помочь вам с этим вопросом.

Для начала, давайте разберемся с данными условиями. У нас есть два треугольника: ∆АВС и ∆А1В1С1. Мы знаем, что первый треугольник относится ко второму треугольнику, то есть ∆АВС : ∆А1В1С1. Также дано, что отношение сторон треугольника ∆АВС равно 9 : 7 : 8.

Теперь перейдем к самому вопросу. У нас есть уравнение x + z = 51​. Нам нужно найти значения x и z. Для этого мы можем использовать отношение сторон треугольника.

Для начала, посмотрим на стороны треугольника ∆АВС. Мы можем представить их через переменные:
AB = 9k
BC = 7k
AC = 8k

Теперь мы должны посмотреть на стороны треугольника ∆А1В1С1. Опять же, мы можем представить их через переменные:
A1B1 = 9k1
B1C1 = 7k1
A1C1 = 8k1

По условию, мы знаем, что ∆АВС : ∆А1В1С1. Это значит, что отношение сторон соответствующих сторон треугольника равно. Мы можем записать это в виде пропорции:
AB/ A1B1 = BC/ B1C1 = AC/ A1C1

Подставляем значения сторон:
(9k)/(9k1) = (7k)/(7k1) = (8k)/(8k1)

Мы можем пренебречь общим множителем k и k1, так как он сократится:
9/9 = 7/7 = 8/8

Заметим, что все значения дробей равны 1. Это значит, что отношения сторон равны. Мы узнали, что отношение AB/ A1B1 = 1, отношение BC/ B1C1 = 1 и отношение AC/ A1C1 = 1.

Теперь мы можем использовать это знание, чтобы решить уравнение x + z = 51​. Поскольку AB/ A1B1 = 1, мы можем сказать, что AB = A1B1. Аналогично, мы можем сказать, что BC = B1C1 и AC = A1C1.

Таким образом, мы можем переписать уравнение x + z = 51​ следующим образом:
AB + BC + A1C1 + B1C1 = 51​

Мы знаем, что AB = A1B1, BC = B1C1 и AC = A1C1, поэтому у нас получается:
AB + BC + AC + AC = 51​

Мы знаем, что AB = 9k, BC = 7k и AC = 8k, поэтому получаем:
9k + 7k + 8k + 8k = 51​

Объединяем подобные слагаемые:
32k = 51​

Теперь, чтобы найти k, мы можем разделить обе стороны уравнения на 32:
k = 51/32

Получаем:
k = 1.59375

Теперь, мы можем найти значения x и z. Мы знаем, что x + z = 51​, поэтому можем подставить значение k:
x + z = 51​
9k + 8k = 51​
17k = 51​

Подставляем значение k:
17(1.59375) = 51​

Решаем уравнение:
27.0625 = 51​

Теперь мы можем найти значения x и z. Подставляем значение k:
x = 9k = 9(1.59375) = 14.34375
z = 8k = 8(1.59375) = 12.75

Итак, мы получили, что x = 14.34375, а z = 12.75.

Надеюсь, я смог подробно объяснить решение этой задачи. Если у вас возникли дополнительные вопросы, пожалуйста, задайте их.